搜索
【题目】如图，在矩形ABCD中，AB＝4，BC＝5，E是BC边上的一个动点，DF⊥AE，垂足为点F，连结CF
（1）若AE＝BC
①求证：△ABE≌△DFA；②求四边形CDFE的周长；③求tan∠FCE的值；
（2）探究：当BE为何值时，△CDF是等腰三角形．
【答案】(1)①证明见解析；②12；③
；(2)当BE为3或2.5或2时，△CDF是等腰三角形．
【解析】
（1）①如图1中，根据AAS证明：△ABE≌△DFA即可．
②利用勾股定理求出BE，即可解决问题．
③如图2中，过点F作FM⊥BC于点M．求出FM，MC即可解决问题．
（2）分三种情形分别求解即可解决问题．
解：(1)①如图1中，
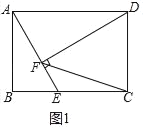
∵四边形ABCD是矩形，
∴AD＝BC，AD∥BC，∠B＝90°，∴∠AEB＝∠DAF．
∵DF⊥AE，∴∠AFD＝90°．
∴∠B＝∠AFD＝90°，
又∵AE＝BC，
∴AE＝AD，
∴△ABE≌△DFA(AAS)．
②如图1中，在Rt△ABE中，∠B＝90°，
根据勾股定理，得 BE＝
＝3，
∵△ABE≌△DFA，
∴DF＝AB＝DC＝4，AF＝BE＝3．
∵AE＝BC＝5，∴EF＝EC＝2，
∴四边形CDFE的周长＝2(DC+EC)＝2×(4+2)＝12．
③如图2中，过点F作FM⊥BC于点M．
，
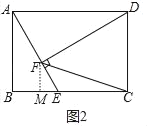
在Rt△FME中， 
，
，
在Rt△FMC中， 
．
(2)如图3﹣1中，当DF＝DC时，则DF＝DC＝AB＝4．
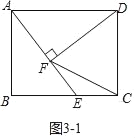
∵∠AEB＝∠DAF，∠B＝∠AFD＝90°，
∴△ABE≌△DFA(AAS)．
∴AE＝AD＝5，
由②可知，BE＝3，∴当BE＝3时，△CDF是等腰三角形．…
如图3﹣2中，当CF＝CD时，过点C作CG⊥DF，垂足为点H，交AD于点G，
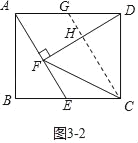
则CG∥AE，DH＝FH．
∴AG＝GD＝2.5．
∵CG∥AE，AG∥EC，
∴四边形AECG是平行四边形，
∴EC＝AG＝2.5，∴当BE＝2.5时，△CDF是等腰三角形．…
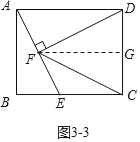
如图3﹣中，当FC＝FD时，过点F作FQ⊥DC，垂足为点Q．
则AD∥FQ∥BC，DQ＝CQ，
∴AF＝FE＝AE．
∵∠B＝∠AFD＝90°，∠AEB＝∠DAF，
∴△ABE∽△DFA，
∴
，即AD×BE＝AF×AE．
设BE＝x，
∴5x＝
，
解得x1＝2，x2＝8(不符合题意，舍去)
∴当BE＝2时，△CDF是等腰三角形．
综上所述，当BE为3或2.5或2时，△CDF是等腰三角形．
