【题目】如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔D、E与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?

参考答案:
【答案】见解析
【解析】分析:根据轮船在点A时两个灯塔与航线的夹角相等可得∠DAB=∠EAB,轮船到达点B时两个灯塔与航线的夹角仍然相等可得∠1=∠2,再根据等角的补角相等推出∠3=∠4,然后利用角边角定理证明△ABD与△ABE全等,然后根据全等三角形对应边相等即可证明.
本题解析:
到达点B时轮船与两个灯塔的距离相等。
理由如下:
根据题意得,∠DAB=∠EAB,∠1=∠2,
∵∠1+∠3=180°,∠2+∠4=180°,
∴∠3=∠4,
在△ABD与△ABE, 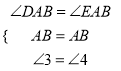 ,
,
∴△ABD≌△ABE(ASA),
∴BD=BE.
即,到达点B时轮船与两个灯塔的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a+5b=10abB.(﹣ab)2=a2bC.2a6÷a3=2a3D.a2a4=a8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0
B.k<2,m<0
C.k>2,m>0
D.k<0,m<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )
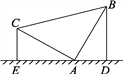
A. 4cm B. 6cm C. 8cm D. 求不出来
-
科目: 来源: 题型:
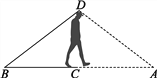
查看答案和解析>>【题目】如图所示,小明为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m.你能猜出河有多宽吗?说说理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明准备完成题目:化简:(□x2+6x+8)-(6x+5x2+2)发现系数“□”印刷不清楚.
(1)她把“□”猜成4,请你化简(4x2+6x+8)-(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”请通过计算说明原题中“□”是几?
-
科目: 来源: 题型:
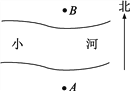
查看答案和解析>>【题目】如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
相关试题

