【题目】解方程:
(1)7y+6=-9y; (2)2(3y-1)-3(2-4y)=9y+10;
(3) y-![]() =2-
=2-![]() ; (4)
; (4)![]() -2+
-2+![]() =3(x-1).
=3(x-1).
参考答案:
【答案】(1)y=-![]() ;(2) y=2;(3) y=
;(2) y=2;(3) y=![]() ;(4) x=
;(4) x=![]() .
.
【解析】
⑴移项,将未知数系数化为1即可求解;⑵去括号,移项,合并同类项,将未知数系数化为1即可求解;⑶去分母,移项,合并同类项,将未知数系数化为1即可求解;⑷去分母,移项,合并同类项,将未知数系数化为1即可求解.
(1)7y+6=-9y,移项,得7y+9y=-6,合并同类项,16y=-6.
系数化为1,得y=-![]() .
.
(2)去括号,得6y-2-6+12y=9y+10.移项得6y+12y-9y=10+2+6,合并同类项,得9y=18,系数化为1,得y=2.
(3)去分母,得6y-3(y-1)=12-(y+2),去括号,得6y-3y+3=12-y-2,移项,得6y-3y+y=12-2-3,合并同类项,得4y=7,系数化为1,得y=![]() .
.
(4)去分母,得2(3x-1)-12+3(2x+4)=18(x-1),去括号,得6x-2-12+6x+12=18x-18,移项,得6x+6x-18x=-18+2+12-12,合并同类项,得-6x=-16,系数化为1,得x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
等级
A级(优秀)
(≥108分)B级(良好)
(≥84分且<108分)C级(及格)
(≥72分且<84分)D级(不及格)
(<72分)人数
22
28
18
根据以上提供的信息解答下列问题:
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
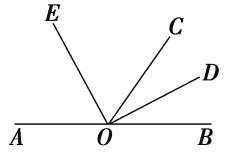
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使D′E和C′E重合,折痕是GE,请探索下列问题:
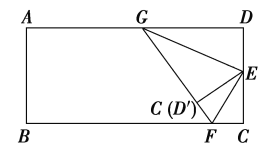
(1)∠FEC′和∠GED′互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些互为余角?哪些互为补角?(各写出两对即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
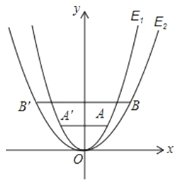
(1)求m的值;
(2)求抛物线E2所表示的二次函数的表达式;
(3)在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
相关试题

