Question

【题目】如图，在四边形ABCD中，已知AB=3，BC=4，CD=12，AD=13，∠B=90°．求四边形ABCD的面积．

Answer 1

【答案】36．

【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．

解：连接AC，如图所示：

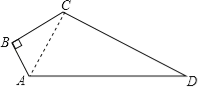
∵∠B=90°，

∴△ABC为直角三角形，

又∵AB=3，BC=4，

∴根据勾股定理得：AC==5，

又∵CD=12，AD=13，

∴AD2=132=169，CD2+AC2=122+52=144+25=169，

∴CD2+AC2=AD2，

∴△ACD为直角三角形，∠ACD=90°，

则S四边形ABCD=S△ABC+S△ACD=ABBC+ACCD=×3×4+×5×12=36．

故四边形ABCD的面积是36．