【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD. 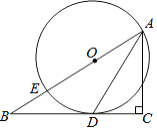
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC= ![]() ,求BD的长.
,求BD的长.
参考答案:
【答案】
(1)解:连接OD.

∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)解:如图2所示:连接ED.

∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC= ![]() ,
,
∴AD= ![]() ×10=4
×10=4 ![]() .
.
∴DC= ![]() ×4
×4 ![]() =4,AC=
=4,AC= ![]() ×4
×4 ![]() =8.
=8.
∵OD∥AC,
∴△BOD∽△BAC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:BD= ![]() .
.
【解析】(1)连接OD.先依据平行线的判定定理证明OD∥AC,然后依据平行线的性质和等腰三角形的性质证明∠OAD=∠DAC,于是可证明AD平分∠BAC.(2)连接ED、OD.由题意可知AE=10.接下来,在△ADA中,依据锐角三角函数的定义可求得AD的长,然后在△ADC中,可求得DC和AC的长,由OD∥AC可证明△BOD∽△BAC,然后由相似三角形的性质可列出关于BD的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题:
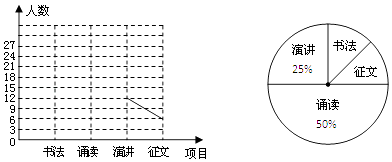
(1)初三(1)班的总人数为 , 扇形统计图中“征文”部分的圆心角度数为度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以40元/千克的进价购进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售价x(元/千克)成一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)若该商店销售这批茶叶的成本不超过2800元,则它的最低销售价应定为多少元?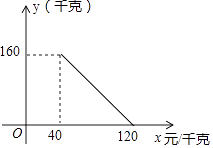
-
科目: 来源: 题型:
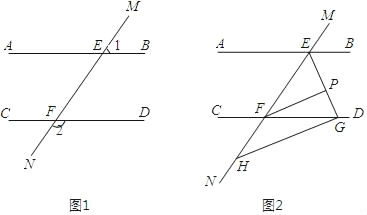
查看答案和解析>>【题目】已知,如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上的一点且GH⊥EG.求证:PF∥GH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
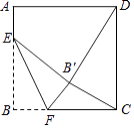
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是________
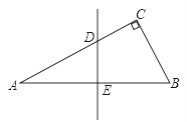
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(﹣2ab)2+a2(a+2b)(a﹣2b)+a8÷a2
(2)解方程:
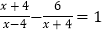
(3)先化简,再求值:
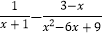 ÷
÷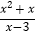 ,其中x=﹣
,其中x=﹣ .
.
相关试题

