【题目】已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°得到△DEC。
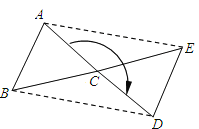
(1)试猜想AE与BD有何关系?说明理由;
(2)请给△ABC添加一个条件,使旋转得到的四边形ABDE为矩形,并说明理由
参考答案:
【答案】(1)AE∥BD,且AE=BD.理由见解析;(2)AC=BC.理由见解析.
【解析】
试题分析:(1)根据旋转的性质推知四边形ABDE是平行四边形,则平行四边形的对边平行且相等,即AE∥BD,且AE=BD;
(2)AC=BC.根据旋转是性质可以推知平行四边形ABDE的对角线AD=BE,则该平行四边形是矩形.
试题解析:(1)AE∥BD,且AE=BD.理由如下:
∵将△ABC绕点C顺时针旋转180°得到△DEC,
∴△ABC≌△DEC,
∴AB=DE,∠ABC=∠DEC,
∴AB∥DE,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD;
(2)AC=BC.理由如下:
∵AC=BC,
∴根据旋转的性质推知AC=BC=CE=CD,
∴AD=BE,
又由(1)知,四边形ABDE是平行四边形,
∴四边形ABDE为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式2a-b-3的值为5,则代数式7+4a-2b的值为________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种油菜籽在相同条件下发芽试验的结果如下:
每批粒数
100
400
800
1 000
2 000
4 000
发芽的频数
85
300
652
793
1 604
3204
发芽的频率
0.850
0.750
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率为___(精确到0.1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集
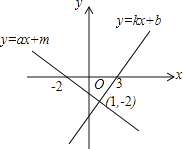
(1)kx+b<ax+m的解集是 ;
(2)
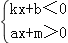 的解集是 ;
的解集是 ;(3)
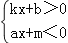 的解集是 ;
的解集是 ;(4)
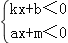 的解集是 .
的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
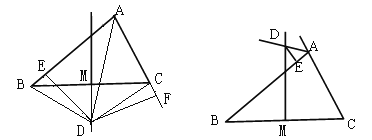
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司最近开发A、B两种型号的手机,一经营手机专卖店销售A、B两种型号的手机,上周销售1部A型3部B型的手机,销售额为8400元.本周销售2部A型1部B型的手机,销售额为5800元.
(1)求每部A型和每部B型手机销售价格各是多少元?
(2)如果某单位拟向该店购买A、B两种型号的手机共6部,发给职工联系业务,购手机费用不少于11200元且不多于11600元,问有哪几种购买方案?
(3)在(2)中哪种方案费用更省?最少费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式ab﹣2ab2﹣a的次数为________
相关试题

