【题目】将一个正方形纸片AOBC放置在平面直角坐标系中，点A（0，4），点O（0，0），B（4，0），C（4，4）点．动点E在边AO上，点F在边BC上，沿EF折叠该纸片，使点O的对应点M始终落在边AC上（点M不与A，C重合），点B落在点N处，MN与BC交于点P．

（Ⅰ）如图①，当∠AEM＝30°时，求点E的坐标；

（Ⅱ）如图②，当点M落在AC的中点时，求点E的坐标；

（Ⅲ）随着点M在AC边上位置的变化，△MPC的周长是否发生变化？如变化，简述理由；如不变，直接写出其值．

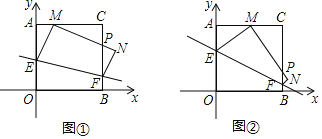
【答案】（Ⅰ）；（Ⅱ）；（Ⅲ）△MPC的周长不变，为8，理由见解析

【解析】

（Ⅰ）由折叠的性质知OE＝EM，设OE＝x，则EM＝OE＝x，AE＝x，根据等量关系AE＋OE＝OA列出方程并解答；

（Ⅱ）由线段中点的定义知AM＝AC＝2．设OE＝m，则EM＝OE＝m，AE＝4﹣m，在Rt△AEM中，由勾股定理列出关于x的方程并解答；

（Ⅲ）设AM＝a，则OE＝EM＝b，MC＝4﹣a，在Rt△AEM中，由勾股定理得出a、b的关系式，可证Rt△AEM∽Rt△CMP，根据相似三角形的周长比等于相似比求△MPC的周长．

解：（Ⅰ）如图①，

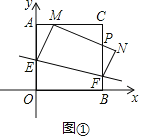
∵四边形ABCD是正方形，

∴∠EAM＝90°．

由折叠知OE＝EM．

设OE＝x，则EM＝OE＝x，

在Rt△AEM中，cos∠AEM＝

∵∠AEM＝30°

∴cos30°＝＝

∴AE＝x，

∴AE＋OE＝OA，即x＋x＝4，

∴x＝16﹣8．

∴

（Ⅱ）如图②，

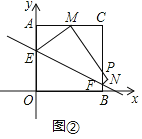
∵点M是边AC的中点，

∴AM＝AC＝2．

设OE＝m，则EM＝OE＝m，AE＝4﹣m，

在Rt△AEM中，EM2＝AM2＋AE2，

即m 2＝22＋（4﹣m）2，解得m＝．

∴；

（Ⅲ）△MPC的周长不变，为8．

理由：设AM＝a，OE＝EM＝b，

∵AC＝4

∴MC＝4﹣a，

在Rt△AEM中，由勾股定理得AE2＋AM2＝EM2，

（4﹣b）2＋a2＝b2，解得16＋a2＝8b．

∴16﹣a2＝8（4﹣b）

∵∠EMP＝90°，∠A＝∠C，

∴Rt△AEM∽Rt△CMP，

∴，即，

解得DM＋MP＋DP＝＝8．

∴△CMP的周长为8．

关闭