
【题目】2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数![]() (人)与时间
(人)与时间![]() (分钟)的变化情况,数据如下表:(表中9-15表示
(分钟)的变化情况,数据如下表:(表中9-15表示![]() )
)
时间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
人数 | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
【答案】(1)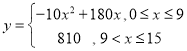 ;(2)队人数最多时是490人,全部考生都完成体温检测需要20.25分钟;(3)至少增加2个检测点
;(2)队人数最多时是490人,全部考生都完成体温检测需要20.25分钟;(3)至少增加2个检测点
【解析】
(1)先根据表中数据的变化趋势猜想:①当![]() 时,
时,![]() 是
是![]() 的二次函数.根据提示设出抛物线的解析式
的二次函数.根据提示设出抛物线的解析式![]() ,再从表中选择两组对应数值,利用待定系数法求函数解析式,再检验其它数据是否满足解析式,从而可得答案;
,再从表中选择两组对应数值,利用待定系数法求函数解析式,再检验其它数据是否满足解析式,从而可得答案;
(2)设第![]() 分钟时的排队人数是
分钟时的排队人数是![]() ,列出
,列出![]() 与第
与第![]() 分钟的函数关系式,再根据函数的性质求排队的最多人数,利用检测点的检测人数列方程求解检测时间;
分钟的函数关系式,再根据函数的性质求排队的最多人数,利用检测点的检测人数列方程求解检测时间;
(3)设从一开始就应该增加![]() 个检测点,根据题意列出不等式,利用不等式在正整数解可得答案.
个检测点,根据题意列出不等式,利用不等式在正整数解可得答案.
解:(1)根据表中数据的变化趋势可知:
①当![]() 时,
时,![]() 是
是![]() 的二次函数.
的二次函数.
∵当![]() 时,
时,![]() ,
,
∴二次函数的关系式可设为![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
将它们分别代入关系式得![]()
解得![]() .
.
∴二次函数的关系式为![]() .
.
将表格内的其他各组对应值代入此关系式,均满足.
②当![]() 时,
时,![]() .
.
∴![]() 与
与![]() 的关系式为
的关系式为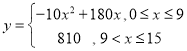 .
.
(2)设第![]() 分钟时的排队人数是
分钟时的排队人数是![]() ,根据题意,得
,根据题意,得
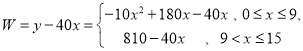
①当![]() 时,
时,![]() .
.
∴当![]() 时,
时,![]() .
.
②当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴![]() .
.
∴排队人数最多时是490人.
要全部考生都完成体温检测,根据题意,
得![]() ,
,
解得![]() .
.
∴排队人数最多时是490人,全部考生都完成体温检测需要20.25分钟.
(3)设从一开始就应该增加![]() 个检测点,
个检测点,
根据题意,得![]() ,
,
解得![]() .
.
∵![]() 是整数,
是整数,
∴![]() 的最小整数是2.
的最小整数是2.
∴一开始就应该至少增加2个检测点.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分B.相等C.互相垂直D.互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月,贵州省积极响应国家“停课不停学”的号召,推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间,随机调查了该校部分初三学生.根据调查结果,绘制出了如下统计图表(不完整),请根据相关信息,解答下列问题:
部分初三学生每天听空中黔课时间的人数统计表
时间/ | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
人数/人 | 2 | 6 | 6 | 10 |
| 4 |
部分初三学生每天听空中黔课时间的人数统计图
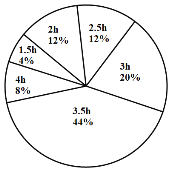
(1)本次共调查的学生人数为_____,在表格中,![]() ___;
___;
(2)统计的这组数据中,每天听空中黔课时间的中位数是____,众数是_____;
(3)请就疫情期间如何学习的问题写出一条你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
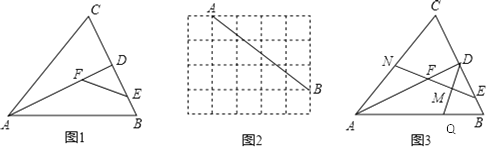
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上.
(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=6,求邻余线AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+2mx+2n,交x轴于A,B两点(A在B的左侧)
(1)当m=3时,n=4时, ①求A、B两点坐标;②将抛物线向右平移k个单位后交x轴于M、N(M在N的左侧),若B、M三等分AN,直接写出k的值;
(2)当m=1时,若线段AB上有且只有5个点的横坐标为整数,求n的取值范围;
(3)记A(x1,0)、B(x2,0),当m、n都是奇数时,x1、x2能否是有理数?若能,请举例验证,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com