【题目】某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
A | 28 | 90% |
B | 40 | 95% |
设种植A种树苗x棵,承包商获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
(3)在达到(2)中政府的要求并获得最大利润的前提下,承包商用绿化队的40人种植这两种树苗,已知每人每天可种植A种树苗6棵或B种树苗3棵,如何分配人数才能使种植A、B两种树苗同时完工.
参考答案:
【答案】(1)y=150000﹣28x﹣40(3000﹣x)=12x+30000(0≤x≤3000).
(2)购买A种树苗1200棵,B种树苗1800棵时,承包商应的利润最大,最大利润为44400元.
(3)安排10人种植A种树苗,30人种植B种树苗,恰好同时完工.
【解析】
试题分析:(1)由购买A种树苗x棵,可得出购买B种树苗(3000﹣x)棵,根据“总利润=报价﹣购买A种树苗钱数﹣购买B种树苗钱数”即可得出y关于x的函数关系式;
(2)根据政府要求栽植这批树苗的成活率不低于93%,即可列出关于x的一元一次不等式,解不等式即可得出x的取值范围,再根据一次函数的性质,即可解决最值问题;
(3)设安排m人种植A种树苗,则有(40﹣m)人种植B种树苗,根据每人每天可种植A种树苗6棵或B种树苗3棵且同时完工,可列出关于m的分式方程,解分式方程求出m的值,检验后即可得出结论.
试题解析:(1)根据题意,得:购买B种树苗(3000﹣x)棵,
∴y与x之间的函数关系式为y=150000﹣28x﹣40(3000﹣x)=12x+30000(0≤x≤3000).
(2)根据题意,得:90%x+95%(3000﹣x)≥93%×3000,
解得:x≤1200,
∵y=12x+30000中k=12>0,
∴当x=1200,3000﹣1200=1800时,y取最大值,最大值为44400.
答:购买A种树苗1200棵,B种树苗1800棵时,承包商应的利润最大,最大利润为44400元.
(3)设安排m人种植A种树苗,则有(40﹣m)人种植B种树苗,
根据题意,得:![]() =
=![]() ,
,
解得:m=10.
经检验,m=10是分式方程的解,且符合实际,此时40﹣10=30(人).
答:安排10人种植A种树苗,30人种植B种树苗,恰好同时完工.
-
科目: 来源: 题型:
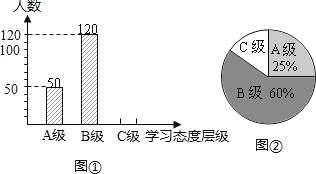
查看答案和解析>>【题目】某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该地8000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A.所有的直角三角形都相似
B.所有的等腰直角三角形都相似
C.所有的菱形都相似
D.所有的矩形都相似 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:对于任意有理数a、b,都有a⊕b=a(a-b)+1,等式的右边是通常的有理数运算,例如2⊕5=2(2-5)+1=2×(-3)+1.
(1)求(-2)⊕3.
(2)若3⊕x=-5,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,﹣3)和点B(3,m),且AB平行于x轴,则点B坐标为( )
A. (3,﹣3) B. (3,3) C. (3,1) D. (3,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 所有的实数都可用数轴上的点表示
B. 三角形的一个外角等于它的两个内角的和
C. 方差能反映一组数据的波动大小
D. 等角的补角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是半径为3的⊙O上的点,
(1)尺规作图:作⊙O的内接正六边形ABCDEF;
(2)求(1)中
 的长.
的长.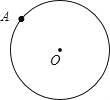
相关试题

