【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
参考答案:
【答案】(1)直拍球拍每副220元,横拍球每副260元;(2)购买直拍球拍30副,则购买横拍球10副时,费用最少.
【解析】(1)设直拍球拍每副x元,根据题中的相等关系:20副直拍球拍的价钱+15副横拍球拍的价钱=9000元;10副横拍球拍价钱-5副直拍球拍价钱=1600元,建立方程组即可求解;
(2)设购买直拍球拍m副,根据题意列出不等式可得出m的取值范围,再根据题意列出费用关于m的一次函数,并根据一次函数的性质解答即可.
解:(1)设直拍球拍每副x元,横拍球每副y元,由题意得,
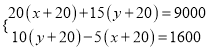
解得, ![]() ,
,
答:直拍球拍每副220元,横拍球每副260元;
(2)设购买直拍球拍m副,则购买横拍球(40-m)副,
由题意得,m≤3(40-m),
解得,m≤30,
设买40副球拍所需的费用为w,
则w=(220+20)m+(260+20)(40-m)
=-40m+11200,
∵-40<0,
∴w随m的增大而减小,
∴当m=30时,w取最小值,最小值为-40×30+11200=10000(元).
答:购买直拍球拍30副,则购买横拍球10副时,费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“同角或等角的补角相等”是( )
A. 定义B. 基本事实C. 定理D. 假命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断正误(对于真命题画“√”,对于假命题画“×”):0是自然数.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O1的半径长为4,⊙O2的半径长为r,圆心距O1O2=6,当⊙O1与⊙O2外切时,r的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
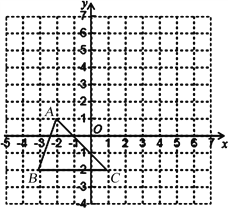
⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM (2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
(1)如图1,在梯形ABCD中,AD∥BC,∠ABC=60°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在给出的网格图上找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.

相关试题

