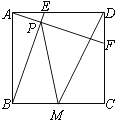
【题目】如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为.
参考答案:
【答案】![]() .
.
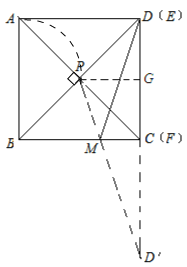
【解析】试题分析:本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.首先作出点D关于BC的对称点D′,从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=2,GD′=6,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.
如图作点D关于BC的对称点D′,连接PD′,由轴对称的性质可知:MD=D′M,CD=CD′=4,
∴PM+DM=PM+MD′=PD′,过点P作PG垂直于C,垂足为G,易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧,当点E与点D重合,点F与点C重合时,PG和GD′均最短, ∴此时PD′最短.
∵四边形ABCD为正方形,
∴PG=![]() AD=2,GC=
AD=2,GC=![]() DC=2.
DC=2.
∴GD′=6.
在Rt△PGD′中,由勾股定理得:PD′=![]() =
=![]() =2
=2![]() .
.
故答案为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,有实数根的是( )
A. x2-x+2=0 B. x2+x-1=0 C. x2-2x+3=0 D. x2+4=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽査了8名参加2019年成都市初中学业水平考试学生的体育成绩,得到的结果如下表:
成绩(分)
46
48
49
50
人数(人)
1
1
2
4
则这8名同学的体育成绩的众数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A.x3﹣x=x(x﹣1)
B.x2﹣y2=(x﹣y)2
C.﹣4x2+9y2=(2x+3y)(2x﹣3y)
D.x2+6x+9=(x+3)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,1)、D(-
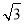 ,0),作直线AD并以线段AD为一边向上作正方形ABCD.
,0),作直线AD并以线段AD为一边向上作正方形ABCD.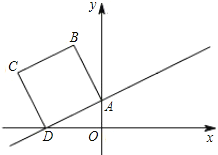
(1)填空:点B的坐标为________,点C的坐标为_________.
(2)若正方形以每秒2个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:
(1)、该校对多少名学生进行了抽样调查?
(2)、图2中x=?.
(3)、若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市教育局为了了解初二学生第一学期参加社会实践活动的天数,随机抽查本市部分初二学生第一学期参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)
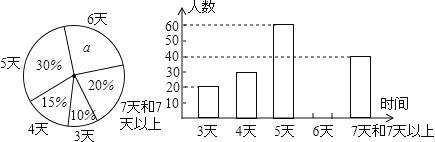
请你根据图中提供的信息,回答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)求实践天数为5天对应扇形的圆心角度数;
(4)如果该市有初二学生20000人,请你估计“活动时间不少于5天”的大约有多少人?
相关试题

