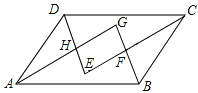
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.

参考答案:
【答案】(1)证明见解析;(2)矩形;(3)![]() .
.
【解析】试题分析:(1)根据角平分线的定义以及平行四边形的性质,即可得到AB=CD,∠BAG=∠DCE,∠ABG=∠CDE,进而判定△ABG≌△CDE;
(2)根据角平分线的定义以及平行四边形的性质,即可得出∠AGB=90°,∠DEC=90°,∠AHD=90°=∠EHG,进而判定四边形EFGH是矩形;
(3)根据含30°角的直角三角形的性质,得到BG,AG,BF,CF,进而得出EF和GF的长,可得四边形EFGH的面积.
试题解析:解:(1)∵GA平分∠BAD,EC平分∠BCD,∴∠BAG=![]() ∠BAD,∠DCE=
∠BAD,∠DCE=![]() ∠DCB,∵ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
∠DCB,∵ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
(2)四边形EFGH是矩形.
证明:∵GA平分∠BAD,GB平分∠ABC,∴∠GAB=![]() ∠BAD,∠GBA=
∠BAD,∠GBA=![]() ∠ABC,∵ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=
∠ABC,∵ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=![]() (∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(3)依题意得,∠BAG=![]() ∠BAD=30°,∵AB=6,∴BG=
∠BAD=30°,∵AB=6,∴BG=![]() AB=3,AG=
AB=3,AG=![]() =CE,∵BC=4,∠BCF=
=CE,∵BC=4,∠BCF=![]() ∠BCD=30°,∴BF=
∠BCD=30°,∴BF=![]() BC=2,CF=
BC=2,CF=![]() ,∴EF=
,∴EF=![]() ﹣
﹣![]() =
=![]() ,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=
,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把数轴上表示数2的点移动4个单位后,表示的数为( )
A.6B.-2C.6或2D.6或-2
-
科目: 来源: 题型:
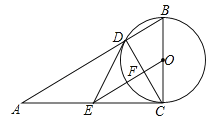
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.
(1)若∠BCD=36°,BC=10,求
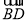 的长;
的长;(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:
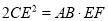 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若BC=20,DE=12,求△MDE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的积为正数,和也为正数,那么这两个数是( )
A.都是正数B.都是负数
C.一正一负,且负数的绝对值大D.一正一负,且正数的绝对值大
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a2+3ab-b2)-(-3+ab+5a2+b2)=5a2■-6b2+3被墨水弄脏了,请问被墨水遮盖住的一项是()
A.+14abB.+3abC.+16abD.+2ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 ( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

