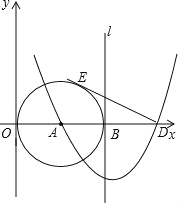
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
参考答案:
【答案】(1)![]()
(2)![]()
(3)BF的长为![]() 或
或![]() .
.
【解析】
试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点坐标式,然后将C点坐标代入求解即可.
(2)由于DE是⊙A的切线,连接AE,那么根据切线的性质知AE⊥DE,在Rt△AED中,AE、AB是圆的半径,即AE=OA=AB=3,而A、D关于抛物线的对称轴对称,即AB=BD=3,由此可得到AD的长,进而可利用勾股定理求得切线DE的长.
(3)若△BFD与EAD△相似,则有两种情况需要考虑:①△AED∽△BFD,②△AED∽△FBD,根据不同的相似三角形所得不同的比例线段即可求得BF的长.
试题解析:(1)设抛物线的解析式为y=a(x﹣6)2+k;
∵抛物线经过点A(3,0)和C(0,9),
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.
(2)连接AE;
∵DE是⊙A的切线,
∴∠AED=90°,AE=3,
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,
∴AB=BD=3,
∴AD=6;
在Rt△ADE中,DE2=AD2﹣AE2=62﹣32=27,
∴![]() .
.
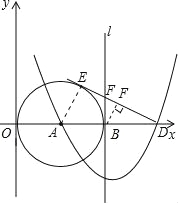
(3)当BF⊥ED时;
∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
当FB⊥AD时,
∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD,
∴![]() ,
,
即![]() ;
;
∴BF的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“全等三角形的对应角相等”的逆命题是:_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= ,BC= ;
(2)判断△ABC与△DEF是否相似?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆.试求预定期限是多少天?计划生产多少辆汽车?
若设预定期限为x天,计划生产y辆汽车,请你根据题意填空,并列出方程组求x与y的值.
(1)若每天生产35辆,在预定期限x天内可生产__________辆,比计划产量y辆汽车__________(“多”或“少”)生产10辆,则可得二元一次方程______________________.
(2)若每天生产40辆,在预定期限x天内可生产__________辆,比计划产量y__________(填“多”或“少”)生产20辆,则可列二元一次方程_________________________.
(3)列方程组_________________________,并解得________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x<y,x2+y2=3,xy=1,则x-y=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红统计了她家3月份的电话通话时间,并绘制成如下的频数分布表(表中数据含最大值但不含最小值):
通话时间(min)
0~2
2~4
4~6
6~8
8~10
通话次数
26
12
8
5
3
那么小红家3月份电话通话时间不超过6min的频数是( )
A.3
B.8
C.38
D.46 -
科目: 来源: 题型:
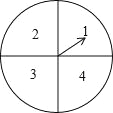
查看答案和解析>>【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
相关试题

