【题目】如图,已知A(﹣4,0.5),B(﹣1,2)是一次函数y=ax+b与反比例函数 ![]() (m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
参考答案:
【答案】
(1)解:当﹣4<x<﹣1时,一次函数大于反比例函数的值
(2)解:把A(﹣4,0.5),B(﹣1,2)代入y=kx+b得,
![]() ,解得
,解得 ![]() ,
,
所以一次函数解析式为y= ![]() x+
x+ ![]() ;
;
把B(﹣1,2)代入 ![]() ,得m=﹣1×2=﹣2
,得m=﹣1×2=﹣2
(3)解:连接PC、PD,如图,

设P点坐标为(t, ![]() t+
t+ ![]() ).
).
∵△PCA和△PDB面积相等,
∴ ![]()
![]() (t+4)=
(t+4)= ![]() 1(2﹣
1(2﹣ ![]() t﹣
t﹣ ![]() ),
),
解得t=﹣ ![]() ,
,
∴P点坐标为(﹣ ![]() ,
, ![]() ).
).
【解析】(1)观察函数图象得到当﹣4<x<﹣1时,一次函数图象都在反比例函数图象上方;(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入 ![]() 可计算出m的值;(3)设P点坐标为(t,
可计算出m的值;(3)设P点坐标为(t, ![]() t+
t+ ![]() ),利用三角形面积公式可得到
),利用三角形面积公式可得到 ![]()
![]() (t+4)=
(t+4)= ![]() 1(2﹣
1(2﹣ ![]() t﹣
t﹣ ![]() ),解方程得到t=﹣
),解方程得到t=﹣ ![]() ,从而可确定P点坐标.
,从而可确定P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在结束了380课时初中阶段数学内容的教学后,李老师计划安排60课时用于总复习.根据数学内容所占课时比例,绘制出如图不完整的统计图表,并且已知“二元一次方程组”和“一元二次方程”教学课时数之和为27课时.请根据以上信息,回答下列问题:

(1)表1中“统计与概率”所对应的课时数为课时,按此推算,在60课时的总复习中,李老师应安排课时复习“统计与概率”内容;
(2)把图2补充完整;
(3)图3中“不等式与不等式组”内容所在扇形的圆心角为度;
表1领域
课时数
数与代数
171
图形与几何
152
统计与概率
?
综合与实践
19
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共
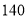 件,进行手绘设计后出售,所获得利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:
件,进行手绘设计后出售,所获得利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:批发价(元)
零售(元)
黑色文化衫
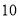
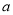
白色文化衫
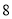
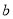
(
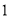 )当
)当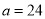 ,
, 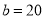 ,假设文化衫全部售出,共获利
,假设文化衫全部售出,共获利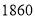 元,求黑白两种文化衫各多少件?
元,求黑白两种文化衫各多少件?(
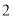 )假设文化衫全部售出,其中卖出了黑色文化衫
)假设文化衫全部售出,其中卖出了黑色文化衫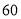 件,要获得
件,要获得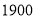 元,请求出
元,请求出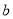 与
与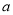 的关系式.
的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】规定一种新的运算a*b=ab+a+b+1,则(﹣3)*4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
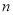 都可以进行这样的分解:
都可以进行这样的分解: 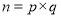 (
(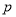 ,
, 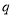 是正整数,且
是正整数,且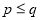 ),在
),在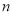 的所有这种分解中,如果
的所有这种分解中,如果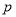 ,
, 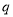 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称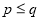 是
是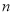 的最佳分解,并规定:
的最佳分解,并规定: 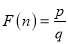 .
.例如
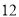 可以分解成
可以分解成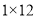 ,
, 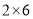 或
或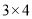 ,因为
,因为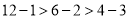 ,所以
,所以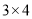 是
是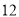 的最佳分解,所以
的最佳分解,所以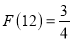 .
.(
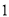 )求出
)求出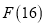 的值.
的值.(
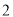 )如果一个两位正整数
)如果一个两位正整数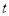 ,
, 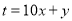 (
(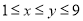 ,
, 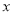 ,
, 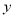 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为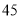 ,那么我们称这个数
,那么我们称这个数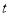 为“文澜数”,求所有“文澜数”并写出所有“文澜数”中
为“文澜数”,求所有“文澜数”并写出所有“文澜数”中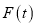 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.张刚按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)张刚在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设张刚获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果张刚想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
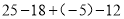
(2)
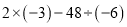
(3)

(4)﹣14﹣2×[5﹣(﹣3)2].
相关试题

