搜索
【题目】如图，等边三角形ABC．请按下列要求解答：
（1）尺规作图：作∠BAC的角平分线交BC于点D，以AD为一边向右侧作等边△ADE（保留作图痕迹，不写作法）．
（2）在（1）的图形上，设AC、DE交于点F，若CF=lcm，求△ABC的周长．
参考答案：
【答案】（1）作图见解析；（2）12cm.
【解析】
（1）按要求作图；
（2）先求得∠DFC=90°，根据直角三角形30度角的性质计算CD的长，从而得AC的长，所以得结论．
解：（1）如图所示：
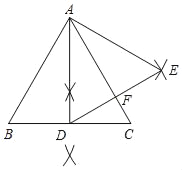
（2）∵△ABC和△ADE是等边三角形，
∴∠BAC=∠C=∠DAE=60°，
∵AD平分∠BAC，
∴AD⊥BC，∠CAD=30°，
∴AC平分∠DAE，
∴AC⊥BE，
∴∠CDF=30°，
∵∠ADE=60°
∴∠DFC=90°
∴CD=2CF=2cm，
∴AC=2CD=4cm，
∴△ABC的周长=4×3=12cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E.
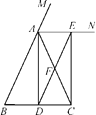
(1)求证：四边形ADCE为矩形；
(2)连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；
(3)线段DF与AB有怎样的关系？请直接写出你的结论．
-
科目： 来源： 题型：
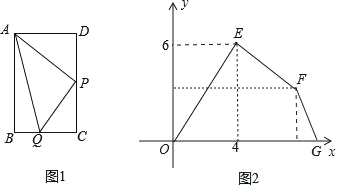
查看答案和解析>>【题目】如图1，在长方形ABCD中，点P是CD中点，点Q从点A开始，沿着A→B→C→P的路线匀速运动，设△APQ的面积是y，点Q经过的路线长度为x，图2坐标系中折线OEFG表示y与x之间的函数关系，点E的坐标为（4，6），则点G的坐标是_____．
-
科目： 来源： 题型：
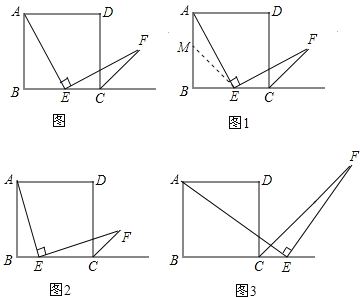
查看答案和解析>>【题目】如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．请你认真阅读下面关于这个图的探究片段，完成所提出的问题．
（1）探究1：小强看到图（*）后，很快发现AE=EF，这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（一个是直角三角形，一个是钝角三角形），考虑到点E是边BC的中点，因此可以选取AB的中点M，连接EM后尝试着去证△AEM≌EFC就行了，随即小强写出了如下的证明过程：
证明：如图1，取AB的中点M，连接EM．
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E，M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC（ASA）
∴AE=EF
（2）探究2：小强继续探索，如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立，请你证明这一结论．
（3）探究3：小强进一步还想试试，如图3，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF是否成立呢？若成立请你完成证明过程给小强看，若不成立请你说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
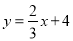与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）
A．（﹣3，0） B．（﹣6，0） C．（
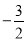，0） D．（
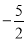，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】小明骑自行车去学校，最初以某一速度匀速行驶，中途自行车发生故障，停下来修车耽误了几分钟，为了按时到校，他加快了速度，仍保持匀速行驶，结果准时到校，到校后，小明画了自行车行进路程s(km)与行进时间t(h)的图象，如图所示，请回答：
(1)这个图象反映了哪两个变量之间的关系？
(2)根据图象填表：
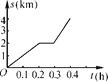
时间t/h
0
0.2
0.3
0.4
路程s/km
(3)路程s可以看成时间t的函数吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点M是线段AB中点，AD、BC交于点N，连接AC、BD、MC、MD，∠l=∠2，∠3=∠4．
（1）求证：△AMD≌△BMC；
（2）图中在不添加新的字母的情况下，请写出除了“△AMD≌△BMC”以外的所有全等三角形，并选出其中一对进行证明．
相关试题
