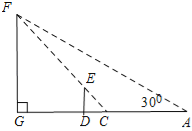
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.

(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,![]() ,结果精确到0.1)
,结果精确到0.1)
参考答案:
【答案】(1)![]() ;(2)12.5米.
;(2)12.5米.
【解析】试题分析:(1)利用△CDE∽△CGF的对应边成比例解答;
(2)通过解利用△CDE∽△CGF来求FG的高度.
解:(1)∵由题意知,FG∥DE,
∴△CDE∽△CGF,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
(2)在直角△AFG中,∠A=30°,![]() ,
,
∵tanA=![]() ,tan30°=
,tan30°=![]() ,
,
即![]() =
=![]() ,
,
解得fg≈12.5.
答:电线杆PQ的高度约12.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系式中,y不是x的函数的是( )
A.y=x2
B.|y|=x
C.y=2x+1
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:xy2﹣4x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2﹣3mxy﹣6y2+12xy﹣9合并后不含xy项,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数值0.0000105用科学记数法表示为( )
A.1.05×104
B.0.105×10﹣4
C.1.05×10﹣5
D.1.05×10﹣7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.
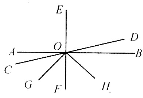
(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连结AE,则△ACE的周长是( )

A.8
B.10
C.14
D.16
相关试题

