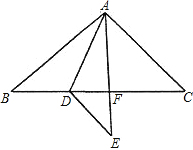
【题目】如图,已知△ABC中,∠B=∠E=40°,∠BAE=60°,且AD平分∠BAE交BC于D.
(1)求证:BD=DE;
(2)若AB=CD,求∠ACD的大小.
参考答案:
【答案】(1)证明见解析;(2)40°
【解析】
(1)要求证:BD=DE可以证明△ABD≌△AED,根据角角边定理就可以证出;
(2)根据AB=AE, AB=CD,得CD=AE,由三角形内角和定理和三角形的外角性质推理可得∠EDC=∠E,则FD=FE,所以CF=AF,再由三角形内角和求出∠ACD.
(1)证明:
∵AD平分∠BAE,
∴∠BAD=∠EAD=30° ,
∵AD=AD,
∵∠B=∠E=40°,
∴△ABD≌△AED ,
∴BD=ED;
(2)解:在△ABD中,
∠ADB=180°﹣∠B﹣∠BAD=110°,
∵△ABD≌△AED,
∴∠ADE=∠ADB=110°,
∵∠ADC=∠B+∠BAD= 70°,
∴∠EDC=∠ADE -∠ADC =110°﹣70°=40°,
∴∠EDC=∠E,
∴FD=FE,
∵AE=AB=CD,
∴EA-EF=DC-DF,
即CF=AF,
∵∠AFC=∠B+∠BAE=60°+40°=100°,
∴∠ACD=![]() (180°-∠AFC)=
(180°-∠AFC)=![]() (180°-100°)= 40°.
(180°-100°)= 40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位在十月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为 4000 元/人,两家旅行社同时又对 10 人以上的团体推出了优惠举 措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位员工的费用,其余员工八 折优惠.
(1)如果设参加旅游的员工共有 n(n>10)人,则甲旅行社的费用为 元,乙旅 行社的费用为 元;(用含 n 的代数式表示)
(2)假如这个单位现组织共 30 名员工到旅游,该单位选择哪一家旅行社比较优惠?请通 过计算说明理由.
(3)如果计划在十月份外出旅游七天,这七天的日期之和(不包含月份)为 105,则他们 于十月 号出发.
-
科目: 来源: 题型:
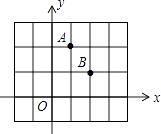
查看答案和解析>>【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得|PA﹣PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OPOQ= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)请直接写出点C关于y轴的对称点C'的坐标: ;
(3)△ABC的面积= ;
(4)在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.
-
科目: 来源: 题型:
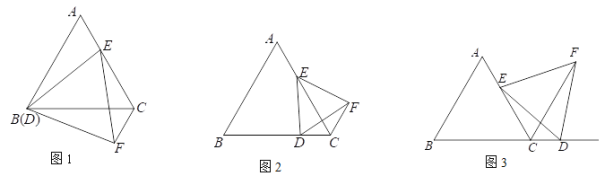
查看答案和解析>>【题目】△ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE为边作等边△DEF,连接CF.
(1)如图1,当点D与点B重合时,求证:△ADE≌△CDF;
(2)如图2,当点D运动到如图2的位置时,猜想CE、CF、CD之间的数量关系,并说明理由;
(3)如图3,当点D在BC延长线上时,直接写出CE、CF、CD之间的数量关系,不证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点 A、B 到表示-2 的点的距离都为 6,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 2 个单位长度,D 点运动速度 为每秒 3 个单位长度,运动时间为 t 秒.
(1)A 点表示数为 ,B 点表示的数为 ,AB= .
(2)若 P 点表示的数是 0,
①运动 1 秒后,求 CD 的长度;
②当 D 在 BP 上运动时,求线段 AC、CD 之间的数量关系式.
(3)若 t=2 秒时,CD=1,请直接写出 P 点表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A.
 B.
B. 
C.
 D.
D. 
相关试题

