【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
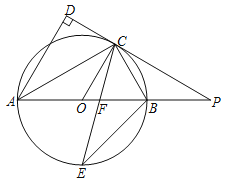
(1)求证:![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
参考答案:
【答案】(1)证明过程见解析;(2)证明过程见解析;(2)24.
【解析】
试题分析:(1)根据切线以及AD⊥PD得出OC∥AD,得到∠ACO=∠DAC,然后根据OC=OA得出∠ACO=∠CAO,从而得到∠DAC=∠CAO,即角平分线;(2)根据题意得出∠PFC=∠PCF,得出PC=PF;(3)根据题意得出△PAC∽△PCB,根据tan∠ABC可得![]() ,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据
,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据![]() 得出k的值,然后求出PC的长度.
得出k的值,然后求出PC的长度.
试题解析:(1)∵PD切⊙O于点C,∴OC⊥PD
又AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.
又OC=OA,∴∠ACO=∠CAO,
∴∠DAC=∠CAO,即AC平分∠DAB.
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°.
又AB为⊙O的直径,∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∠DAC=∠CAO,∴∠CAO=∠PCB.
∵CE平分∠ACB,∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴PC=PF
(3)∵∠PAC=∠PCB,∠P=∠P,
∴△PAC∽△PCB,
∴![]() .
.
又tan∠ABC=![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,
,![]() ,则在Rt△POC中,
,则在Rt△POC中,![]() ,
,
∵AB=14,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴k=6 (k=0不合题意,舍去).
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A. 50° B. 45° C. 40° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A. (5,3) B. (﹣1,﹣2) C. (﹣1,﹣1) D. (0,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54﹣x=20%×108
B.54﹣x=20%(108+x)
C.54+x=20%×162
D.108﹣x=20%(54+x) -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形至少有( )
A. 一个锐角 B. 两个锐角 C. 一个钝角 D. 一个直角
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A=50°,∠B=60°,则∠C=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 相等的角是对顶角; B. a、b、c是直线,若a//b,b//c,则a//c;
C. 同位角相等; D. a、b、c是直线,若a⊥b,b⊥c,则a⊥c。
相关试题

