【题目】在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
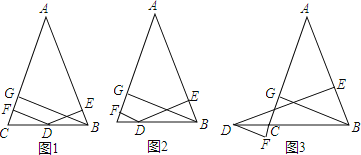
(1)、如图1,若D是BC边上的中点,∠A=45°,DF=3,求AC的长;
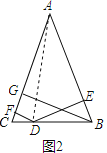
(2)、如图2,D是线段BC上的任意一点,求证:BG=DE+DF;
(3)、在图3,D是线段BC延长线上的点,猜想DE、DF与BG的关系,并证明.
参考答案:
【答案】(1)、AC=6![]() ;(2)、证明过程见解析;(3)、DE﹣DF=BG;证明过程见解析.
;(2)、证明过程见解析;(3)、DE﹣DF=BG;证明过程见解析.
【解析】
试题分析:(1)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出BG=DE+DF,根据角平分线的性质得出BG=6,根据等腰直角三角形的性质得出AC的长度;(2)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出线段之间的关系;(3)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出线段之间的关系.
试题解析:(1)、如图1,连结AD.则△ABC的面积=△ABD的面积+△ACD的面积,
即![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() ACBG, ∵AB=AC,∴DE+DF=BG, ∵D是BC边上的中点,∴AD平分∠BAC,
ACBG, ∵AB=AC,∴DE+DF=BG, ∵D是BC边上的中点,∴AD平分∠BAC,
∴DE=DF=3,∴BG=6, ∵∠A=45°,∴△AGB是等腰直角三角形, ∴AB=![]() BG=6
BG=6![]() ,∴AC=6
,∴AC=6![]() ;
;
(2)、如图2,连结AD.则△ABC的面积=△ABD的面积+△ACD的面积,
即![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() ACBG, ∵AB=AC,∴DE+DF=BG;
ACBG, ∵AB=AC,∴DE+DF=BG;
(3)、DE﹣DF=BG,
如图3,连接AD,则△ABC的面积=△ABD的面积﹣△ACD的面积, 即![]() ABDE﹣
ABDE﹣![]() ACDF=
ACDF=![]() ACBG,
ACBG,
∵AB=AC,∴DE﹣DF=BG.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据为:25,25,27,27,26,则其平均数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有限个,其中正确的结论是( )
A.①②
B.②③
C.③④
D.②③④ -
科目: 来源: 题型:
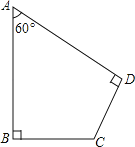
查看答案和解析>>【题目】如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.
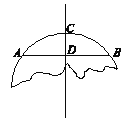
(1)求作此残片所在的⊙O(不写作法,保留作图痕迹);
(2)已知AB=12cm,(1)中⊙O的直径为20cm,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x3=x5
B.(x+y)2=x2+y2
C.x2x3=x6
D.(x2)3=x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】为判断某运动员的成绩是否稳定,教练要对他10 次训练的成绩进行统计分析,则教练需了10 次成绩的
A. 众数 B. 方差 C. 平均数 D. 频数
相关试题

