【题目】用“☆”定义一种新运算:对于任意有理数a和b , 规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(﹣
☆3)☆(﹣ ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m , ( ![]() x)☆3=n(其中x为有理数),试比较m , n的大小.
x)☆3=n(其中x为有理数),试比较m , n的大小.
参考答案:
【答案】
(1)解:(﹣2)☆3=﹣2×32+2×(﹣2)×3+(﹣2)=﹣32
(2)解: ![]() ☆3=
☆3= ![]() ×32+2×
×32+2× ![]() ×3+
×3+ ![]() =8a+8,
=8a+8,
则![]()
=2a+2,
即2a+2=8
解得:a=3
(3)解:已知等式整理得:2x2+4x+2=m, ![]() ,即4x=n,
,即4x=n,
则m﹣n=2x2+2 所以,m>n
【解析】(1)根据所给的新运算列式计算;
(2)按照所给的新运算列式方程,解方程求得a的值;
(3)根据所给的新运算列出关于m、n的式子,再求差可比较得答案.
-
科目: 来源: 题型:
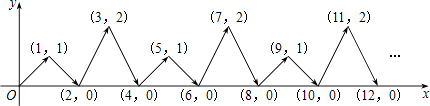
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线
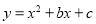 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线x=t与x轴相交于点H.
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为
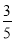 ,求此时t的值.
,求此时t的值.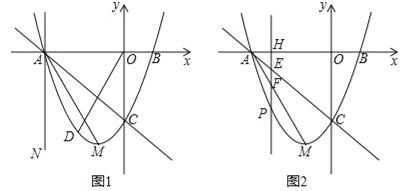
-
科目: 来源: 题型:
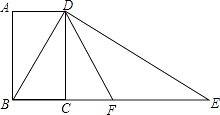
查看答案和解析>>【题目】如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,求x2+(y﹣4)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两条边的长分别为5cm和8cm,则它的周长是( )
A.13cm
B.18cm
C.21cm
D.18cm或21cm -
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A’B’C’,且△ABC与△A’B’C’的面积之比为1:4,则相似比为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】福建省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
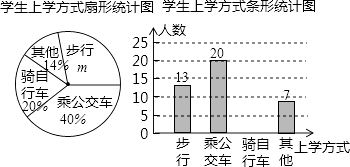
(1)m=%,这次共抽取名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有6000名学生,请你估计该校骑自行车上学的学生有多少名?
相关试题

