【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.

参考答案:
【答案】(1)220;110;(2)∠E+∠F=180°.理由见解析;(3)AB∥CD.
【解析】试题分析:(1)先根据三角形内角和定理求出∠FBC+∠BCF=180°-∠F=110°,再由角平分线定义得出∠ABC=2∠FBC,∠BCD=2∠BCF,那么∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;由四边形ABCD的内角和为360°,得出∠BAD+∠CDA=360°-(∠ABC+∠BCD)=140°.由角平分线定义得出∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,那么∠DAE+∠ADE=
∠CDA,那么∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(2)由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°,由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°,又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,于是∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)由(2)可知∠E+∠F=180°,如果∠E=∠F,那么可以求出∠E=∠F=90°,根据三角形内角和定理求出∠DAE+∠ADE=90°,再利用角平分线定义得到∠BAD+∠CDA=180°,于是AB∥CD.
试题解析:(1)∵∠F=70,
∴FBC+∠BCF=180°∠F=110°.
∵∠ABC、∠BCD的角平分线交于点F,
∴∠ABC=2∠FBC,∠BCD=2∠BCF,
∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;
∵四边形ABCD的内角和为360°,
∴∠BAD+∠CDA=360°(∠ABC+∠BCD)=140°.
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,
∴∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,
∠CDA,
∴∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,
(∠BAD+∠CDA)=70°,
∴∠E=180°(∠DAE+∠ADE)=110°;
故答案为:220;110;
(2)∠E+∠F=180°.理由如下:
∵∠BAD+∠CDA+∠ABC+∠BCD=360°,
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F,
∴∠DAE+∠ADE+∠FBC+∠BCF=180°,
∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,
∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,
∴∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)AB∥CD.
-
科目: 来源: 题型:
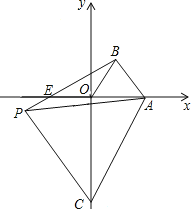
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(a,0)(a>0),点C是y轴上的一个动点,点C在y轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边△AOB(此时点P与点B重合).
(1)点C在移动的过程中,当等边三角形ACP的顶点P在第三象限时(如图所示),求证:△AOC≌△ABP;
(2)若点P在第三象限,BP交x轴于点E,且∠ACO=20°,求∠PAE的度数和E点的坐标;
(3)若∠APB=30°,则点P的横坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
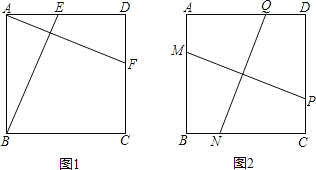
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
-
科目: 来源: 题型:
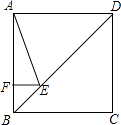
查看答案和解析>>【题目】正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心
 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段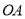 、(2)半圆弧
、(2)半圆弧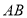 、(3)线段
、(3)线段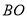 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离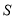 (蚂蚁所在位置与
(蚂蚁所在位置与 点之间线段的长度)与时间
点之间线段的长度)与时间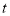 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率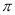 的值取3)
的值取3)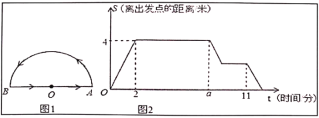
(1)请直接写出:花坛的半径是 米,
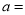 .
.(2)当
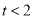 时,求
时,求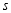 与
与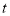 之间的关系式;
之间的关系式;(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回
 所用时间.
所用时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
相关试题

