【题目】阅读以下内容,并回答问题:
若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是 命题(填“真”或“假”);
(2)在△ABC中,已知∠C=90°,△ABC的内角∠A、∠B、∠C所对边的长分别为a、b、c,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
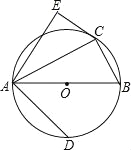
(3)如图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A、B不重合),D是半圆![]() 的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
参考答案:
【答案】(1)真(2)![]() (3)证明见解析
(3)证明见解析
【解析】
试题分析:(1)直接根据奇异三角形的定义直接得出结论;
(2)先根据勾股定理得出a2+b2=c2,再由Rt△ABC是奇异三角形,且b>a可知a2+c2=2b2,把a当作已知条件表示出b,c的值,进而可得出结论;
(3)连接BD,根据圆周角定理得出∠ACB=∠ADB=90°,在Rt△ACB与在Rt△ADB中可得出AC2+BC2=AB2,AD2+BD2=AB2,根据点D是半圆![]() 的中点,得出
的中点,得出![]() .故可得出AD=BD.通过等量代换可得出AC2+CB2=2AD2.再由CB=CE,AE=AD可得出AC2+CE2=2AE2故可得出结论.
.故可得出AD=BD.通过等量代换可得出AC2+CB2=2AD2.再由CB=CE,AE=AD可得出AC2+CE2=2AE2故可得出结论.
试题解析:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
∴等边三角形一定是奇异三角形是真命题.
故答案为:真;
(2)∵∠C=90°,
∴a2+b2=c2①.
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②.
由①②得:b=![]() a,c=
a,c=![]() a.
a.
∴a:b:c=![]() .
.
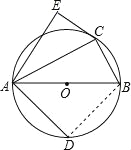
(3)连接BD.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆![]() 的中点,
的中点,
∴![]() .
.
∴AD=BD.
∴AB2=AD2+BD2=2AD2.
∴AC2+CB2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,世界上能制造出的最小晶体管的长度只有0.000 000 04m,将0.000 000 04用科学记数法表示为( )
A.4×108
B.4×10﹣8
C.0.4×108
D.﹣4×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是36°,则该正多边形为( )
A.正八边形B.正九边形C.正十边形D.正十一边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在战“疫”诗歌创作大赛中,有7名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前3名,除要了解自己的成绩外,还要了解这7名同学成绩的( )
A.中位数B.平均数C.众数D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠):
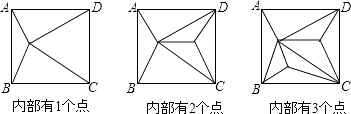
(1)填写如表:正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是( )
A.
清华大学
B.
浙江大学
C.
北京大学
D.
中南大学
相关试题

