【题目】如图,锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() .
.
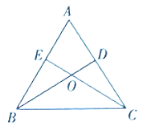
(1)证明:![]() .
.
(2)判断点![]() 是否在
是否在![]() 的角平分线上,并说明理由.
的角平分线上,并说明理由.
(3)连接![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
参考答案:
【答案】(1)见解析(2)点O在∠BAC的角平分线上,理由见解析(3)平行,理由见解析
【解析】
(1)根据题意证明△BCE≌△CBD即可求解;
(2)由(1)得到△ABC为等腰三角形,连接AO并延长交BC于F,通过证△AOE≌△AOD,得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(3)连接![]() ,根据等腰三角形三线合一即可求解.
,根据等腰三角形三线合一即可求解.
(1)∵锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]()
BC=CB,
∴△BCE≌△CBD(HL)
∴![]()
(2)解:点O在∠BAC的角平分线上.
理由:∵△BCE≌△CBD
∴∠EBC=∠DCB,BE=CD
∴△ABC为等腰三角形,
∴AB=AC,
则AB-BE=AC-CD
∴AE=AD
连接AO并延长交BC于F,
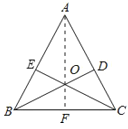
在Rt△AOE和Rt△AOD中,
![]()
∴Rt△AOE≌Rt△AOD.
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
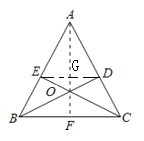
(3)平行,理由如下:
如图,连接![]() ,交AF于G点,
,交AF于G点,
∵AE=AD
∴△ADE为等腰三角形,
由(2)得到AF为∠BAC的角平分线
∴AG⊥DE,
又AF⊥BC,
∴DE∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】精准扶贫,助力苹果产业大发展.甲、乙两超市为响应党中央将消除贫困和实现共同富裕作为重要的奋斗目标,到种植苹果的贫困山区分别用
 元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果
元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果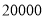 千克,以进价的
千克,以进价的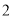 倍价格销售,剩下的小苹果以高于进价的
倍价格销售,剩下的小苹果以高于进价的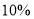 销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利
销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利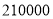 元(包含人工工资和运费).
元(包含人工工资和运费).(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①GP=GD;②∠BAD=∠ABC;③点P是△ACQ的外心;④
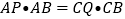 .其中正确的是______________(填序号)
.其中正确的是______________(填序号)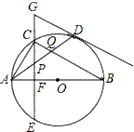
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 绕点
绕点 顺时针旋转得到
顺时针旋转得到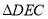 ,使点
,使点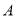 的对应点
的对应点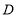 恰好落在边
恰好落在边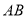 上,点
上,点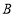 的对应点为
的对应点为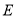 ,连接
,连接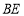 ,其中有:①
,其中有:①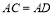 ;②
;②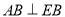 ;③
;③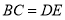 ;④
;④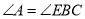 ,四个结论,则结论一定正确的有( )个
,四个结论,则结论一定正确的有( )个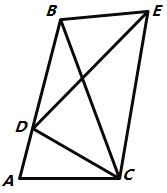
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行力四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图.
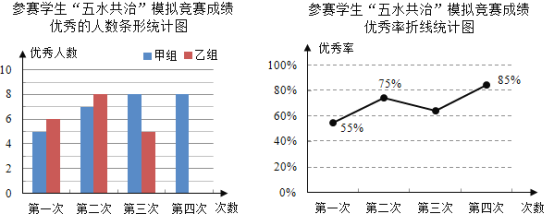
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数
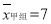 ,方差
,方差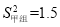 ,请通过计算说明,哪一组成绩优秀的人数比较稳定?
,请通过计算说明,哪一组成绩优秀的人数比较稳定?
相关试题

