【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
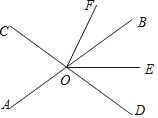
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
参考答案:
【答案】(1)∠BOF=33°;(2)∠AOC=72°;(3) ∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,∠BOF=(
α°,∠BOF=(![]() )°+
)°+![]() α°.
α°.
【解析】试题分析:
(1)由∠AOC=76°易得∠BOD=76°,结合OE平分∠BOD可得∠DOE=∠BOE=38°,由此可得∠COE=180°-38°=142°,结合OF平分∠COE可得∠EOF=71°,最后由∠BOF=∠EOF-∠BOE即可求得∠BOF的度数;
(2)设∠BOE=x,由OE平分∠BOD,∠AOC=∠BOD可得∠DOE=∠BOE=x,∠AOC=2x,结合∠BOF=36°,OF平均∠EOF可得∠COF=∠EOF=x+36°,最后由∠AOC+∠COF+∠BOF=180°即可列出关于x的方程,解方程求得x的值即可求得∠AOC的度数;
(3)设∠BOE=x,则由已知条件易得∠AOC=2x,∠BOF=90°-![]() x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
试题解析:
(1)∵∠BOD=∠AOC=76°,
又∵OE平分∠BOD,
∴∠DOE=![]() ∠BOD=
∠BOD=![]() ×76°=38°.
×76°=38°.
∴∠COE=180°﹣∠DOE=180°﹣38°=142°,
∵OF平分∠COE,
∴∠EOF=![]() ∠COE=
∠COE=![]() ×142°=71°,
×142°=71°,
∴∠BOF=∠EOF﹣∠BOE=71°﹣38°=33°.
(2)∵OE平分∠BOD,OF平分∠COE,
∴∠BOE=∠EOD,∠COF=∠FOE,
∴设∠BOE=x,则∠DOE=x,
故∠COA=2x,∠EOF=∠COF=x+36°,
则∠AOC+∠COF+∠BOF=2x+x+36°+36°=180°,
解得:x=36°,
故∠AOC=72°.
(3)设∠BOE=x,
∵OE平分∠BOD,∠BOD=∠AOC,
∴∠DOE=x,∠COA=2x,
∴∠BOC=180°-2x,
∴∠COE=180°-x,
∵OF平分∠COE,
∴∠EOF=90°-![]() x,
x,
∴∠BOF=90°﹣![]() x,
x,
∵|∠AOC﹣∠BOF|=α°,
∴|2x﹣(90°﹣![]() x)|=α°,
x)|=α°,
解得:x=(![]() )°+
)°+![]() α°或x=(
α°或x=(![]() )°﹣
)°﹣![]() α°,
α°,
当x=(![]() )°+
)°+![]() α°时,
α°时,
∠AOC=2x=(![]() )°+
)°+![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°﹣
)°﹣![]() α°;
α°;
当x=(![]() )°﹣
)°﹣![]() α°时,
α°时,
∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°+
)°+![]() α°.
α°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年毕节市参加中考的学生约为115000人,将115000用科学记数法表示为( )
A.1.15×106
B.0.115×106
C.11.5×104
D.1.15×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
-
科目: 来源: 题型:
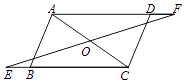
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1),△ABC的面积为
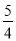 。
。 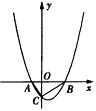
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是( )
A.﹣3B.﹣1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形而不是中心对称图形的是( )
A.圆B.等腰三角形C.平行四边形D.梯形
相关试题

