搜索
【题目】体育委员统计了七（1）班全体同学60秒跳绳的次数，并列出下面的频数分布表：
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | 2 | 4 | 21 | 14 | 7 | 3 | 1 |
给出以下结论：①全班有52个学生； ②组距是20； ③组数是7；④跳绳次数在100≤x<140范围的学生约占全班学生的67%.其中正确结论的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
参考答案：
【答案】D
【解析】参加跳绳活动的总人数为:2+4+21+14+7+3+1=52(人)，故①正确；
根据频数分布表可知组距为20，组数为7，故②、③正确；
跳绳次数x在100≤x＜140范围的同学有21+14=35(人),占全班同学的
×100%≈67.3%，故④正确.
所以正确结论的个数是4个.
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某新品种葡萄试验基地种植了10亩新品种葡萄，为了解这些新品种葡萄的单株产量，从中随机抽查了4株葡萄，在这个统计工作中，4株葡萄的产量是( )
A. 总体 B. 总体中的一个样本 C. 样本容量 D. 个体
-
科目： 来源： 题型：
查看答案和解析>>【题目】_________的绝对值是它本身．
-
科目： 来源： 题型：
查看答案和解析>>【题目】调查某班级的学生对数学老师的喜欢程度，下列最具有代表性的样本是( )
A. 调查单数学号的学生 B. 调查所有的班级干部
C. 调查全体女生 D. 调查数学兴趣小组的学生
-
科目： 来源： 题型：
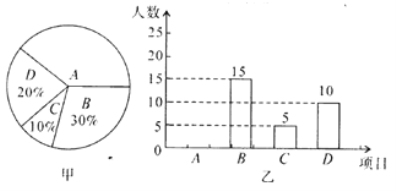
查看答案和解析>>【题目】某中学开展课外体育活动，决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种)，随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题.
(1) 样本中最喜欢A项目的人数所占的百分比为 ；
(2) 请把条形统计图补充完整;
(3) 若该校有学生1700人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】【背景】已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1，d2，d3，且d1＝d3＝1，d2＝2.我们把四个顶点分别在l，m，n，k这四条平行线上的四边形称为“格线四边形” ．
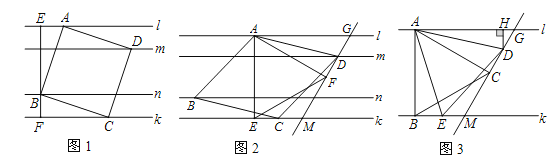
【探究1】(1)如图1，正方形ABCD为“格线四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F.求正方形ABCD的边长．
【探究2】(2)如图2，菱形ABCD为“格线四边形”且∠ADC＝60°，△AEF是等边三角形，AE⊥k于点E，∠AFD＝90°，直线DF分别交直线l，k于点G、点M.求证：EC＝DF．
【拓展】(3)如图3，l∥k，等边△ABC的顶点A，B分别落在直线l，k上，AB⊥k于点B，且∠ACD＝90°，直线CD分别交直线l、k于点G、点M，点D、点E分别是线段GM、BM上的动点，且始终保持AD＝AE，DH⊥l于点H.猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．
求证：
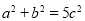．该同学仔细分析后，得到如下解题思路：
先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故
，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证．（1）请你根据以上解题思路帮尤秀同学写出证明过程．
（2）利用题中的结论，解答下列问题：
在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求
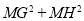的值．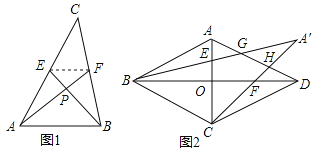
相关试题
