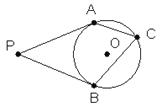
【题目】如图, PA、PB是⊙O的切线,切点为A、B,C是⊙O上一点(P与A、B不重合),若∠P=52°,则∠ACB=______________度.
参考答案:
【答案】64或116
【解析】
连接OA、OB.根据切线的性质,得到∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB,再进一步根据圆周角定理求解即可,同列得出C点在劣弧AB上时,求出∠ACB的度数即可.
连接OA、OB,
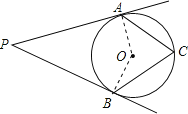
∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°(切线的性质).
∵∠P=52°(已知),
∴∠AOB=180°-∠P=128°(四边形的内角和定理),
∴∠ACB=![]() ∠AOB=64°(同弧所对的圆周角是所对的圆心角的一半).
∠AOB=64°(同弧所对的圆周角是所对的圆心角的一半).
同理可得出:当C点在劣弧AB上时,∠ACB的度数为:180°-64°=116°.
故答案为:64或116.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点
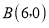 的直线
的直线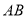 与直线
与直线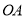 相交于点
相交于点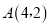 ,动点
,动点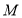 在线段
在线段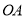 和射线
和射线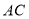 上运动.
上运动.(1)求直线
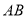 的解析式.
的解析式.(2)求
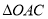 的面积.
的面积.(3)是否存在点
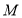 ,使
,使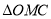 的面积是
的面积是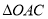 的面积的
的面积的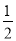 ?若存在求出此时点
?若存在求出此时点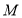 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.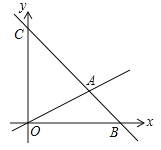
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元)
50
60
70
80
销售数量y(万件)
5.5
5
4.5
4
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)育德中学800名学生参加第二十届运动会开幕式大型表演,道具选用红黄两色锦绣手幅.已知红色手幅每个4元;黄色手幅每个2.5元;购买800个道具共花费2420元,那么两种手幅各多少个?
(2)学校计划制作1000个吉祥物作为运动会纪念.现有甲、乙两个工厂可以生产这种吉祥物.
甲工厂报价:不超过400个时每个吉祥物20元,400个以上超过部分打七折;但因生产条件限制,截止到学校交货日期只能完成800个;乙工厂报价每个吉祥物18元,但需运费400元.问:学校怎样安排生产可以使总花费最少,最少多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】精准扶贫,助力苹果产业大发展.甲、乙两超市为响应党中央将消除贫困和实现共同富裕作为重要的奋斗目标,到种植苹果的贫困山区分别用
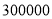 元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果
元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果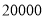 千克,以进价的
千克,以进价的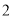 倍价格销售,剩下的小苹果以高于进价的
倍价格销售,剩下的小苹果以高于进价的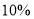 销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利
销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利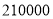 元(包含人工工资和运费).
元(包含人工工资和运费).(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
相关试题

