搜索
【题目】已知：如图，在△ABC中，∠B=90
，∠ACB=30，AB=2，AD=2AC，DC=2BC．
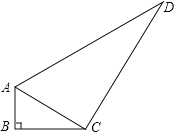
（1）求证：△ACD为直角三角形；（2）求四边形ABCD的面积．
参考答案：
【答案】（1）证明见解析；（2）
．
【解析】
（1）根据勾股定理求出BC的长度，再根据勾股定理逆定理得出△ACD为直角三角形；
（2）根据四边形ABCD的面积=△ABC的面积+△ACD的面积，列式进行计算即可得解．
（1）在Rt△ABC中，∵∠ACB=30°，AB=2，∴AC=2AB=4（在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半）．
在Rt△ABC中，∵∠B=90°，∴BC2+AB2=AC2（勾股定理），∴
．
∵AD=2AC，DC=2BC，∴AD=8，
，∴AC2+CD2=16+48=64，AD2=64，∴AD2=AC2+CD2，∴△ACD为直角三角形，∠ACD=90°（勾股定理逆定理）．
（2）∵S四边形ABCD=S△ABC+S△ACD，∴
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知等边三角形ABC的顶点B、C的坐标分别为（0，0）和（0，4）．
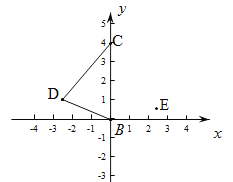
（1）求顶点A的坐标．
（2）D为第二象限内一点，作出点P，使得P到DB和DC的距离相等，且到点E的距离等于DB（不写作法，保留作图痕迹）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为( )
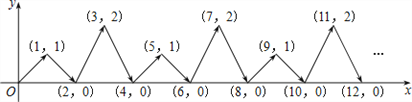
A. （2017，1） B. （2017，0） C. （2017，2） D. （2016，0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD是BC边上的中线，∠BAC=150
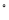，∠CAD=120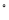．求证：AC=2AD．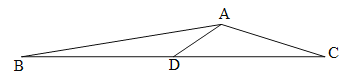
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线L：y＝x2＋x－6与x轴相交于A、B两点（点A在点B的左侧），并与y轴相交于点C．
(1)求A、B、C三点的坐标，并求出△ABC的面积；
(2)将抛物线向左或向右平移，得到抛物线L，且L与x轴相交于A、B两点（点A在点B的左侧），并与y轴交于点C，要使△ABC和△ABC的面积相等，求所有满足条件的抛物线的函数表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出
(1)如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为 ．
问题探究
(2)如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值．
问题解决
(3)如图③所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°．新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F．也就是，分别在
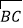、线段AB和AC上选取点P、E、F．由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)．
图① 图② 图③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足
＋|b－6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O－C－B－A－O的线路移动．（1）a＝______________，b＝_____________，点B的坐标为_______________；
（2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标；
（3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．
相关试题
