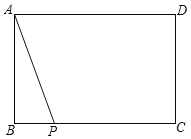
【题目】如图，已知矩形ABCD中，AB=3，BC=5，P是线段BC上的一动点．

（1）请用不带刻度的直尺和圆规，按下列要求作图：（不要求写作法，但保留作图痕迹），在CD边上确定一点E，使得∠DEP+∠APB=180°；

（2）在（1）的条件下，点P从点B移动到点C的过程中，对应点E随之运动，则移动过程中点E经过的总路程长为 ．

【答案】（1）答案见解析；（2）．

【解析】

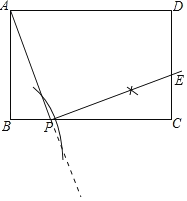
（1）过点P作PE⊥PA交CD于E，点E即为所求．

（2）设PB＝x，EC＝y，利用相似三角形的性质构建二次函数，利用二次函数的性质解决问题即可．

（1）如图点E即为所求．

（2）设PB=x，EC=y．

∵四边形ABCD是矩形，

∴AB=CD=3，BC=AD=5，∠B=∠C=90°．

∵∠APE=90°，

∴∠APB+∠EPC=90°，∠EPC+∠PEC=90°，

∴∠APB=∠PEC，

∴△ABP∽△PCE，

∴，

∴，

∴y=﹣x2+=﹣（x﹣）2+．

∵﹣＜0，

∴x=时，y有最大值，最大值为，

观察图象可知：当点P从B运动到C时，CE的值从0增加到，然后逐渐减小到0，

∴点E的运动路径的长=2×=．

故答案为：．

关闭