搜索
【题目】如图，已知一次函数与反比例函数的图象交于点A（﹣4，﹣2）和B（a，4）． 
（1）求反比例函数的解析式和点B的坐标；
（2）根据图象回答，当x在什么范围内时，一次函数的值大于反比例函数的值？
参考答案：
【答案】
（1）解：设反比例函数的解析式为y= 
（k≠0），
∵反比例函数图象经过点A（﹣4，﹣2），
∴﹣2= 
，
∴k=8，
∴反比例函数的解析式为y= 
，
∵B（a，4）在y= 的图象上，
∴4= 
，
∴a=2，
∴点B的坐标为B（2，4）
（2）解：根据图象得，当x＞2或﹣4＜x＜0时，一次函数的值大于反比例函数的值
【解析】（1）设反比例函数解析式为y= ，把点A的坐标代入解析式，利用待定系数法求反比例函数解析式即可，把点B的坐标代入反比例函数解析式进行计算求出a的值，从而得到点B的坐标；（2）写出一次函数图象在反比例函数图象上方的x的取值范围即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在数轴上有A，B两点，所表示的数分别为
，
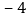，点A以每秒5个单位长度的速度向右运动，同时点B以每秒3个单位长度的速度也向右运动，如果设运动时间为t秒，解答下列问题：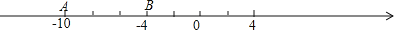
运动前线段AB的长为______；运动1秒后线段AB的长为______；
运动t秒后，点A，点B运动的距离分别为______和______；
求t为何值时，点A与点B恰好重合；
在上述运动的过程中，是否存在某一时刻t，使得线段AB的长为5，若存在，求t的值；若不存在，请说明理由． -
科目： 来源： 题型：
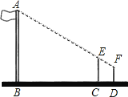
查看答案和解析>>【题目】在一次数学活动课上，小芳到操场上测量旗杆的高度，她的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图)，然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，利用她所测数据，求旗杆的高．
-
科目： 来源： 题型：
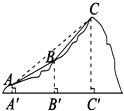
查看答案和解析>>【题目】如图，点A、B、C表示某旅游景区三个缆车站的位置，线段AB、BC表示连接缆车站的钢缆，已知A、B、C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米、310米、710米，钢缆AB的坡度i1=1：2，钢缆BC的坡度i2=1：1，景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？（注：坡度i是指坡面的铅直高度与水平宽度的比）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b与反比例函数
的图像交于A(2，4)，B(-4，n)两点，交x轴于点C．
(1)求m、n的值；
(2)请直接写出不等式kx+b＜
的解集；(3)将x轴下方的图像沿x轴翻折，点B落在点B′处，连接AB′、B′C，求△A B′C的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在数轴l上，一动点Q从原点O出发，沿直线l以每秒钟2个单位长度的速度来回移动，其移动方式是先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…
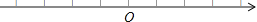
（1）求出5秒钟后动点Q所处的位置；
（2）如果在数轴l上还有一个定点A，且A与原点O相距20个单位长度，问：动点Q从原点出发，可能与点A重合吗？若能，则第一次与点A重合需多长时间？若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】)矩形
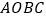中，
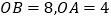.分别以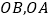
所在直线为
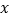轴，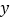
轴，建立如图1所示的平面直角坐标系.
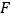是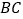
边上一个动点(不与
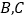重合)，过点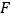的反比例函数y=
(
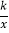)的图像与边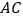
交于点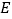
.
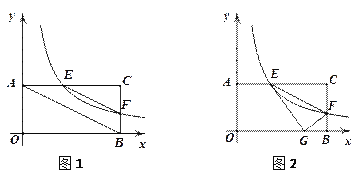
(1)当点
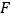运动到边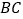的中点时，求点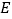的坐标；(2)连接EF、AB，求证：EF∥AB；
(3)如图2，将
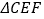沿
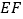折叠，点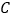
恰好落在边
上的点
处，求此时反比例函数的解析式.
相关试题
