Question

【题目】（1）问题发现

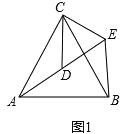
如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．

填空：

①∠AEB的度数为___________；

②线段AD，BE之间的数量关系为___________．

（2）拓展探究

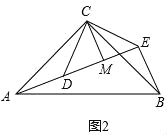
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

（3）解决问题

如图3，在正方形ABCD中，CD=，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．

Answer 1

【答案】（1）①60°；②AD=BE；（2）∠AEB=90°，AE=BE+2CM，理由见解析；（3）或．

【解析】

试题分析：（1）①如图1，∵△ACB和△DCE均为等边三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°．∴∠ACD=∠BCE．在△ACD和△BCE中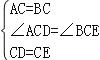，，∴△ACD≌△BCE（SAS）．∴∠ADC=∠BEC．∵△DCE为等边三角形，∴∠CDE=∠CED=60°．∵点A，D，E在同一直线上，∴∠ADC=120°．∴∠BEC=120°．∴∠AEB=∠BEC﹣∠CED=60°．故答案为：60°．

②∵△ACD≌△BCE，∴AD=BE．故答案为：AD=BE．

（2）∠AEB=90°，AE=BE+2CM．理由：如图2，∵△ACB和△DCE均为等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°．∴∠ACD=∠BCE．在△ACD和△BCE中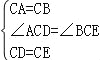，，∴△ACD≌△BCE（SAS）．∴AD=BE，∠ADC=∠BEC．∵△DCE为等腰直角三角形，∴∠CDE=∠CED=45°．∵点A，D，E在同一直线上，∴∠ADC=135°．∴∠BEC=135°．∴∠AEB=∠BEC﹣∠CED=90°．∵CD=CE，CM⊥DE，∴DM=ME．∵∠DCE=90°，∴DM=ME=CM．∴AE=AD+DE=BE+2CM．

（3）点A到BP的距离为或．理由如下：∵PD=1，∴点P在以点D为圆心，1为半径的圆上．∵∠BPD=90°，∴点P在以BD为直径的圆上．∴点P是这两圆的交点．

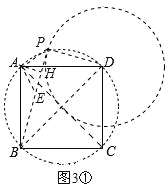
①当点P在如图3①所示位置时，连接PD、PB、PA，作AH⊥BP，垂足为H，过点A作AE⊥AP，交BP于点E，如图3①．∵四边形ABCD是正方形，∴∠ADB=45°．AB=AD=DC=BC=，∠BAD=90°．∴BD=2．∵DP=1，∴BP=．∵∠BPD=∠BAD=90°，∴A、P、D、B在以BD为直径的圆上，∴∠APB=∠ADB=45°．∴△PAE是等腰直角三角形．又∵△BAD是等腰直角三角形，点B、E、P共线，AH⊥BP，∴由（2）中的结论可得：BP=2AH+PD．∴=2AH+1．∴AH=．

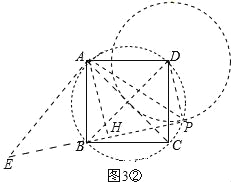
②当点P在如图3②所示位置时，连接PD、PB、PA，作AH⊥BP，垂足为H，过点A作AE⊥AP，交PB的延长线于点E，如图3②．同理可得：BP=2AH﹣PD．∴=2AH﹣1．∴AH=．综上所述：点A到BP的距离为或．