【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.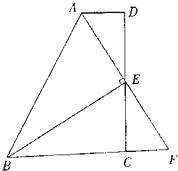
求证:
(1)FC=AD
(2)AB=BC+AD.
参考答案:
【答案】
(1)
解:(1)∵AD∥BC,∴∠ADC=∠ECF,∵E是CD的中点,∴DE=EF,∵在△ADE与△FCE中,∠ADC=∠ECF,DE=EF,∠AED=∠CEF,∴△ADE≌△FCE(ASA),∴FC=AD;
(2)
解:∵△ADE≌△FCE,∴AE=EF,AD=CF,又∵BE⊥AE,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF,∵AD=CF,∴AB=BC+AD.
【解析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲看乙的方向是北偏东40°,那么乙看甲的方向是_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号(把你认为正确结论的序号都填上)
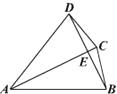
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
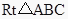 中,∠C=90°,∠A=30°.
中,∠C=90°,∠A=30°.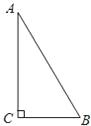
(1)尺规作图:作线段AB的垂直平分线l(保留作图痕迹,不写作法);
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a+2|+(b﹣1)2=0,那么(a+b)2019的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(m,n﹣2)与点B(﹣2,n)关于原点对称,则点A的坐标为_____.
相关试题

