【题目】如图,一抛物线型拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1米后,水面的宽度为米. 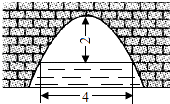
参考答案:
【答案】2 ![]()
【解析】解:如图, 
建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(﹣2,0),
到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣1代入抛物线解析式得出:
﹣1=﹣0.5x2+2,
解得:x=± ![]() ,
,
所以水面宽度增加到2 ![]() 米,
米,
故答案为:2 ![]() 米.
米.
根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=﹣1代入抛物线解析式得出水面宽度,即可得出答案.此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①若a<1,则(a﹣1)
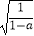 =﹣
=﹣ 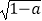 ;②平行四边形既是中心对称图形又是轴对称图形;③
;②平行四边形既是中心对称图形又是轴对称图形;③ 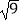 的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3 , 若AD=2,AB=2
 ,∠A=60°,则S1+S2+S3的值为( )
,∠A=60°,则S1+S2+S3的值为( ) 
A.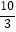
B.
C.
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣
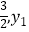 ),(
),( 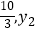 )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 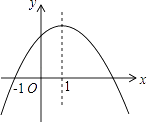
A.①②
B.②③
C.②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:打折前,买 10 件 A 商品和 5 件 B 商品共用了 400 元,买 5 件 A 商品和 10件 B 商品共用了 350 元.
(1)求打折前 A 商品、B 商品每件分别多少钱?
(2)打折后,买 100 件 A 商品和 100 件 B 商品共用了 3800 元.比不打折少花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
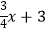 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 . 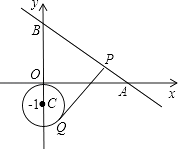
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知﹣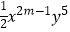 与xnym+n是同类项,求m、n的值;
与xnym+n是同类项,求m、n的值;
(2)先化简后求值:( )
)  ,其中a=
,其中a= 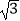 .
.
相关试题

