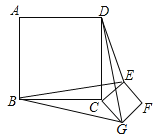
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③![]() ,其中正确结论是 (填序号)
,其中正确结论是 (填序号)
参考答案:
【答案】①②③.
【解析】
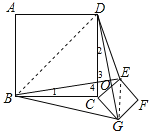
试题分析:设BE,DG交于O,∵四边形ABCD和EFGC都为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,在△BCE和△DCG中,∵BC=DC,∠BCE=∠DCG,CE=CG,∴△BCE≌△DCG(SAS),∴BE=DG,∴∠1=∠2,∵∠1+∠4=∠3+∠1=90°,∴∠2+∠3=90°,∴∠BOC=90°,∴BE⊥DG;故①②正确;
连接BD,EG,如图所示,∴DO2+BO2=BD2=BC2+CD2=2a2,EO2+OG2=EG2=CG2+CE2=b2,则BG2+DE2=DO2+BO2+EO2+OG2=2a2+b2,故③正确.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
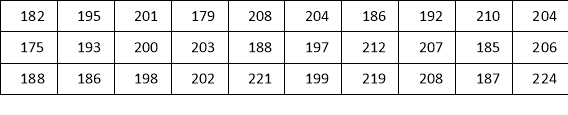
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
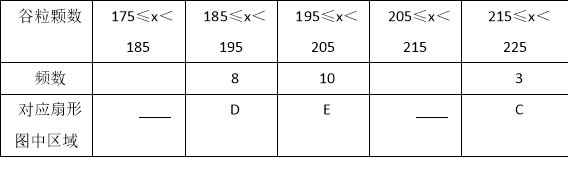
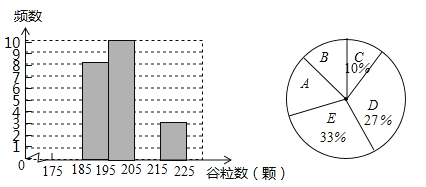
如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:

下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2+kxy+9y2是完全平方式,则k的值是_______________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距600千米,快车的速度是60千米/小时,慢车的速度是40千米/小时,两车分别从甲、乙两地同时出发,相向而行,_____小时后两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一项工程预计在规定的日期内完成,如果甲独做刚好能完成,如果乙独做就要超过日期3天,现在甲、乙两人合做2天,剩下的工程由乙独做,刚刚好在规定的日期完成,问规定日期是几天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.

相关试题

