练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

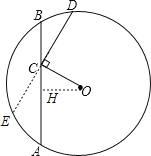
    【题目】如图所示，动点C在⊙O的弦AB上运动，AB=，连接OC，CD⊥OC交⊙O于点D．则CD的最大值为 ．

    【答案】．

    【解析】

    试题分析：作OH⊥AB，延长DC交⊙O于E，如图，根据垂径定理得到AH=BH=AB=，CD=CE，再利用相交弦定理得CDCE=BCAC，易得CD=，当CH最小时，CD最大，C点运动到H点时，CH最小，所以CD的最大值为．

    解：作OH⊥AB，延长DC交⊙O于E，如图，

    ∴AH=BH=AB=，

    ∵CD⊥OC，

    ∴CD=CE，

    ∵CDCE=BCAC，

    ∴CD2=（BH﹣CH）（AH+CH）=（﹣CH）（+CH）=3﹣CH2，

    ∴CD=，

    ∴当CH最小时，CD最大，

    而C点运动到H点时，CH最小，

    此时CD=，即CD的最大值为．

    故答案为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解方程：（1）2(1-x)2-8=0 （2）2x2x-1=0 (3)x2-3x+1=0(配方法)

    （4）（x+3)(x－1)＝5. (5) （x-1）2-5（x-1）+6=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（1）aa3﹣a6÷a2 ；（2）（x+2）（x+1）﹣2x（x﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．

    （1）=　　．

    （2）如图2，当△CEF绕点C顺时针旋转a时（0°＜a＜180°），连结AF，BE，求线段BE与线段AF的位置关系和。

    （3）如图3，当△CEF绕点C顺时针旋转a时（0°＜a＜180°），延长FC交AB于点D，如果AD=6﹣2，求旋转角a的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】化简：(3x﹣y)(y+3x)﹣(4x﹣3y)(4x+3y)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l1、l2（如图①）．

    （1）在图②的平面直角坐标系中，画出到直线y=x＋2的距离为1的所有点的集合的图形．并写出该图形与y轴交点的坐标．

    （2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线y= x ＋ 2的距离为1的点的个数与r的关系．

    （3）如图③，若以坐标原点O为圆心，2为半径的圆上只有两个点到直线y= x ＋ b的距离为1，则b的取值范围为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若∠1与∠2互补，∠3与30°互余，∠2+∠3=200°，则∠1=____度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题是假命题的是（ ）

    A. 在同一平面内，过一点有且只有一条直线与已知直线垂直

    B. 对顶角相等

    C. 两直线平行，同位角相等

    D. 同旁内角互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边三角形的边长为4，点是边上一动点(不与点重合)，以为边在的下方作等边三角形，连接.

    (1)在运动的过程中， 与有何数量关系?请说明理由.

    (2)当时，求的度数.

    查看答案和解析>>

    同步练习册答案