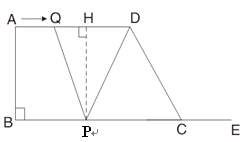
如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t(秒)．
（1）当t为何值时，四边形PQDC是平行四边形．
（2）当t为何值时，以C，D，Q，P为顶点的梯形面积等于60cm2？
（3）是否存在点P，使△PQD是等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由．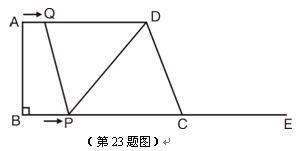

（1）∵四边形PQDC是平行四边形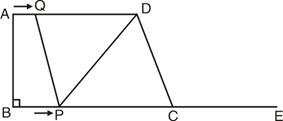

∴DQ=CP
∵DQ=AD－AQ=16－t，CP=21－2t
∴16－t=21－2t
解得 t="5"
当 t=5秒时，四边形PQDC是平行四边形
…………（4分）
（2）若点P，Q在BC，AD上时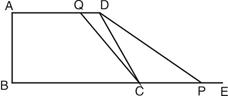

 

 
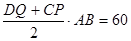        即

       解得t＝9（秒）  …………（2分）
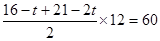
若点P在BC延长线上时，则CP="2t-21,"
∴
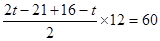
解得 t＝15（秒）
∴当t＝9或15秒时，以C，D，Q，P为顶点的梯形面积等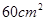（2分）
（3）当PQ＝PD时
作PH⊥AD于H，则HQ=HD

∵QH=H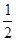D=QD=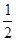（16-t）
由AH=BP得 
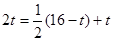
解得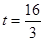秒  …………（2分）
当PQ=QD时  QH=AH－AQ=BP－AQ＝2t－t="t," QD=16-t
∵QD2= PQ2=122+t2
∴（16--t）2=122+t2 解得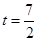(秒) …………（2分）
当QD=PD时  DH="AD" -AH=AD-BP=16-2t
∵QD2=PD2=PH2+HD2=122+(16-2t)2
∴(16-t)2=122+(16-2t)2
即  3t2-32t+144=0
∵△＜0
∴方程无实根
综上可知,当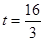秒或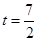(秒)时, △BPQ是等腰三角形……（2分）

解析

关闭