【题目】如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
参考答案:
【答案】解:过点C作CD⊥AB交AB延长线于一点D,
根据题意得∠BAC=30°,∠BCA=15°,
故∠DBC=∠DCB=45°,
在Rt△ADC中,
∵AC=400米,∠BAC=30°,
∴CD=BD=200米,
∴BC=200 ![]() 米,AD=200
米,AD=200 ![]() 米
米
∴AB=AD﹣BD=(200 ![]() ﹣200)米,
﹣200)米,
∴三角形ABC的周长为400+200 ![]() +(200
+(200 ![]() ﹣200)≈829米
﹣200)≈829米
小金沿三角形绿化区的周边小路跑一圈共跑了约829米.
【解析】延长AB至D点,作CD⊥AD于D,根据题意得∠BAC=30°,∠BCA=15°,利用三角形的外角的性质得到∠DBC=∠DCB=45°,然后在Rt△ADC中,求得CD=BD=200米后即可求得三角形ABC的周长.
【考点精析】利用关于方向角问题对题目进行判断即可得到答案,需要熟知指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.
-
科目: 来源: 题型:
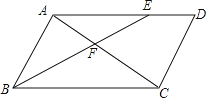
查看答案和解析>>【题目】如图,在ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F,若
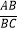 =
= 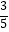 ,则
,则 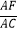 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为 .
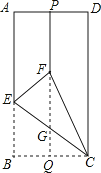
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
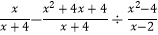 ,其中x=2sin60°﹣(
,其中x=2sin60°﹣(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,
 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:(1)求
 =________.
=________.(2)若
 =5,则x=____.
=5,则x=____.(3)同理
 表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得 =3,这样的整数是________(直接写答案)
=3,这样的整数是________(直接写答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先观察下列等式,再完成题后问题:
 ,
, ,
,
①请你猜想:
 =________.
=________.②若a、b为有理数,且
 ,
,求:
 +…+
+…+ 的值.
的值.(2)探究并计算:
 +
+ +
+ +…+
+…+
(3)如图,把一个面积为1的正方形等分成两个面积为
 的长方形,接着把面积为
的长方形,接着把面积为 的长方形等分成两个面积为
的长方形等分成两个面积为 的正方形,再把面积为
的正方形,再把面积为 的正方形等分成两个面积为
的正方形等分成两个面积为 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算: +
+ +
+ +
+ +
+ +
+ +
+ .(直接写答案).
.(直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了更好地活跃校园文化生活,拟对本校自办的“辉煌”校报进行改版.先从全校学生中随机抽取一部分学生进行了一次问卷调查,题目为“你最喜爱校报的哪一个板块”(每人只限选一项).问卷收集整理后绘制了不完整的频数分布表和如图扇形统计图.
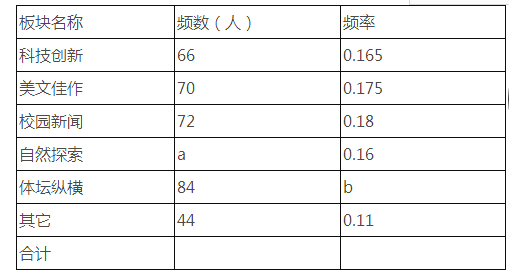
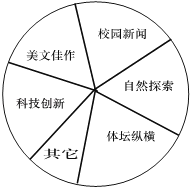
(1)填空:频数分布表中a= , b=;
(2)“自然探索”板块在扇形统计图中所占的圆心角的度数为;
(3)在参加此次问卷调查的学生中,最喜爱哪一个板块的人数最多?有多少人喜欢?
(4)若全校有1500人,估计喜欢“校园新闻”板块的有多少人?
相关试题

