Question

【题目】如图，已知AB∥CD，点E在直线AB，CD之间．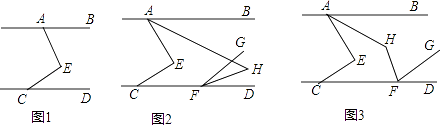

（1）求证：∠AEC=∠BAE+∠ECD；
（2）若AH平分∠BAE，将线段CE沿CD平移至FG．
①如图2，若∠AEC=90°，HF平分∠DFG，求∠AHF的度数；
②如图3，若HF平分∠CFG，试判断∠AHF与∠AEC的数量关系并说明理由．

Answer 1

【答案】
（1）解：如图1，过点E作直线EN∥AB，

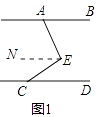
∵AB∥CD，

∴EN∥CD，

∴∠BAE=∠AEN，∠DCE=∠CEN，

∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD

（2）解：∵AH平分∠BAE，

∴∠BAH=∠EAH，

①∵HF平分∠DFG，设∠GFH=∠DFH=x，

又CE∥FG，

∴∠ECD=∠GFD=2x，

又∠AEC=∠BAE+∠ECD，∠AEC=90°，

∴∠BAH=∠EAH=45°﹣x，

如图2，过点H作l∥AB，

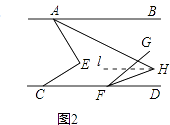
易证∠AHF=∠BAH+∠DFH=45°﹣x+x=45°；

②设∠GFD=2x，∠BAH=∠EAH=y，

∵HF平分∠CFG，

∴∠GFH=∠CFH=90°﹣x，

由（1）知∠AEC=∠BAE+∠ECD=2x+2y，

如图3，过点H作l∥AB，

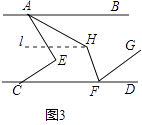
易证∠AHF﹣y+∠CFH=180°，

即∠AHF﹣y+90°﹣x=180°，∠AHF=90°+（x+y），

∴∠AHF=90°+ ∠AEC．（或2∠AHF﹣∠AEC=180°．）

【解析】（1）过E作EF∥AB，可得∠A=∠AEF，利用平行于同一条直线的两直线平行得到EF与CD平行，再得到一对内错角相等，进而得出答案；（2）①HF平分∠DFG，设∠GFH=∠DFH=x，根据平行线的性质可以得到∠AHF的度数；②设∠GFD=2x，∠BAH=∠EAH=y，根据角平分线的性质以及平行线的性质即可得到∠AHF与∠AEC的数量关系．
【考点精析】认真审题，首先需要了解平行线的性质(两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补)，还要掌握平移的性质(①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等)的相关知识才是答题的关键．