【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为a. 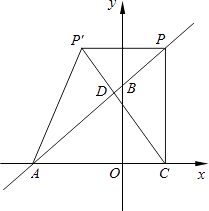
(1)当b=3时, ①求直线AB的解析式;
②若点P′的坐标是(﹣1,m),求m的值;
(2)若点P在第一象限,记直线AB与P′C的交点为D.当P′D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P′CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:①设直线AB的解析式为y=kx+3,
把x=﹣4,y=0代入得:﹣4k+3=0,
∴k= ![]() ,
,
∴直线的解析式是:y= ![]() x+3,
x+3,
②P′(﹣1,m),
∴点P的坐标是(1,m),
∵点P在直线AB上,
∴m= ![]() ×1+3=
×1+3= ![]()
(2)解:∵PP′∥AC,
△PP′D∽△ACD,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴a= ![]()
(3)解:以下分三种情况讨论.
①当点P在第一象限时,
(i)若∠AP′C=90°,P′A=P′C(如图1)
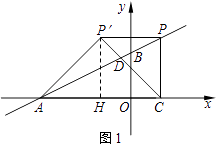
过点P′作P′H⊥x轴于点H.
∴PP′=CH=AH=P′H= ![]() AC.
AC.
∴2a= ![]() (a+4)
(a+4)
∴a= ![]()
∵P′H=PC= ![]() AC,△ACP∽△AOB
AC,△ACP∽△AOB
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴b=2
(ii)若∠P′AC=90°,(如图2),

则四边形P′ACP是矩形,则PP′=AC.
若△PCA为等腰直角三角形,则:P′A=CA,
∴2a=a+4
∴a=4
∵P′A=PC=AC,△ACP∽△AOB
∴ ![]() =1,即
=1,即 ![]() =1
=1
∴b=4
(iii)若∠P′CA=90°,
则点P′,P都在第一象限内,这与条件矛盾.
∴△P′CA不可能是以C为直角顶点的等腰直角三角形.
②当点P在第二象限时,∠P′CA为钝角(如图3),
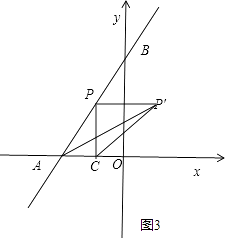
此时△P′CA不可能是等腰直角三角形;
③当P在第三象限时,∠P′AC为钝角(如图4),此时△P′CA不可能是等腰直角三角形.
所有满足条件的a,b的值为: ![]() ,
, ![]() .
.

【解析】(1)①利用待定系数法即可求得函数的解析式;②把(﹣1,m)代入函数解析式即可求得m的值;(2)可以证明△PP′D∽△ACD,根据相似三角形的对应边的比相等,即可求解;(3)分P在第一,二,三象限,三种情况进行讨论.利用相似三角形的性质即可求解.
【考点精析】掌握等腰直角三角形和确定一次函数的表达式是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B,连接OA.
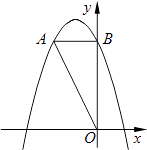
(1)求△OAB的面积;
(2)若抛物线y=﹣x2﹣2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】2011年5月20日是第22个中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如图).根据信息,解答下列问题.
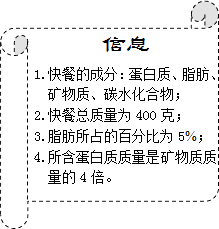
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物质量的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O.下列条件中,不能判断对角线互相垂直的是( )
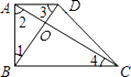
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.OB2+OC2=BC2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2018的坐标是( )

A. (5,3) B. (3,5) C. (0,2) D. (2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
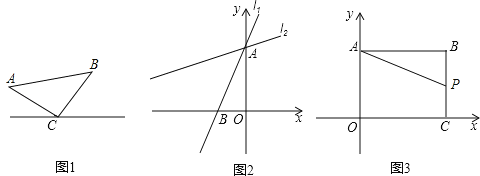
(1)如图2,在直角坐标系中,直线l1:y=
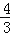 x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
相关试题

