【题目】已知![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的动点(
上的动点(![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() .
.
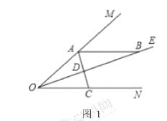
(1)如图1,若![]() ,则:
,则:
①![]() 的度数为
的度数为
②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
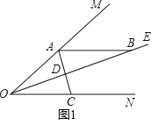
(2)如图2,若![]() ,则是否存在这样的
,则是否存在这样的![]() 的值,使得
的值,使得![]() 中有两个想等的角?若存在,求出
中有两个想等的角?若存在,求出![]()
参考答案:
【答案】(1)①24°,②108,54;(2)存在,x=42、24、33、123.
【解析】
(1)①运用平行线的性质以及角平分线的定义,可得①∠ABO的度数;②根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;
(2)分两种情况进行讨论:AC在AB左侧,AC在AB右侧,分别根据三角形内角和定理以及直角的度数,可得x的值.
(1)如图1,
①∵∠MON=48°,OE平分∠MON,
∴∠AOB=∠BON=24°,
∵AB∥ON,
∴∠ABO=24°;
②当∠BAD=∠ABD时,∠BAD=24°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°24°×3=108°;
当∠BAD=∠BDA时,∵∠ABO=24°,
∴∠BAD=78°,∠AOB=24°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°24°24°78°=54°,
故答案为:①24°;②108,54;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角.

∵AB⊥OM,∠MON=48°,OE平分∠MON,
∴∠AOB=24°,∠ABO=66°,
①当AC在AB左侧时:
若∠BAD=∠ABD=66°,则∠OAC=90°66°=24°;
若∠BAD=∠BDA=![]() (180°66°)=57°,则∠OAC=90°57°=33°;
(180°66°)=57°,则∠OAC=90°57°=33°;
若∠ADB=∠ABD=66°,则∠BAD=48°,故∠OAC=90°48°=42°;
②当AC在AB右侧时:
∵∠ABE=114°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=![]() (180°114°)=33°,则∠OAC=90°+33°=123°.
(180°114°)=33°,则∠OAC=90°+33°=123°.
综上所述,当x=24、33、42、123时,△ADB中有两个相等的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形
 (记作
(记作 )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 ,
, ,
, ,先将
,先将 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到 .
.
(1)在图中画出
 ;
;(2)点
 ,
, 的坐标分别为______、______;
的坐标分别为______、______;(3)若
 轴有一点
轴有一点 ,使
,使 与
与 面积相等,求出
面积相等,求出 点的坐标.
点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。

(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
-
科目: 来源: 题型:
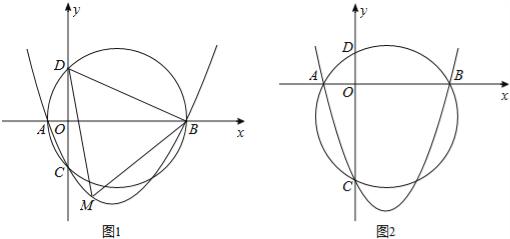
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察下列各式:


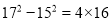 ……
……你发现了什么规律?试用你发现的规律填空:
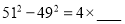 ;
;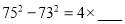
(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:两个等腰直角三角形(
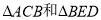 )边长分别为a和b(
)边长分别为a和b( )如图放置在一起,连接AD,
)如图放置在一起,连接AD,
(1)求阴影部分(
 )的面积
)的面积 (2)如果有一个
 点正好位于线段
点正好位于线段 的中点,连接
的中点,连接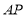 .
. 得到
得到 ,求
,求 的面积
的面积(3)(2)中的三角形
 比(1)中的
比(1)中的 面积大还是小,大(小)多少?
面积大还是小,大(小)多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
用时的频数 用时
线路



合计
3路
260
167
23
450
121路
160
166
124
450
26路
50
122
278
450
早高峰期间,乘坐__________(“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
相关试题

