【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.点P从点A出发,以每秒5个单位
长度的速度沿AC方向运动,过点P作PQ⊥AB于点Q,当点Q和点B重合时,点P停止运动,以AP和AQ为边作APHQ.设点P的运动时间为t秒(t>0)
(1)线段PQ的长为 .(用含t的代数式表示)
(2)当点H落在边BC上时,求t的值.
(3)当APHQ与△ABC的重叠部分图形为四边形时,设四边形的面积为S,求S与t之间的函数关系式.
(4)过点C作直线CD⊥AB于点D,当直线CD将APHQ分成两部分图形的面积比为1:7时,直接写出t的值.

参考答案:
【答案】(1)4t;(2)t=![]() ;(3)当0<t≤
;(3)当0<t≤![]() 时, S=12t2,当
时, S=12t2,当![]() ≤t≤
≤t≤![]() 时,S==﹣
时,S==﹣![]() t2+
t2+![]() t;(4)t的值为
t;(4)t的值为![]() 或
或![]() s.
s.
【解析】
(1)利用勾股定理求出BC,再根据sinA=![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)如图2中,因为QH∥AC,可得![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
(3)两种情形分别求解:①如图3中,当0<t≤![]() 时,重叠部分是四边形APHQ.②如图4中,当
时,重叠部分是四边形APHQ.②如图4中,当![]() ≤t≤
≤t≤![]() 时,重叠部分是四边形ACMQ;
时,重叠部分是四边形ACMQ;
(4)两种情形画出图形分别利用三角形的中位线定理求解即可;
(1)如图1中,
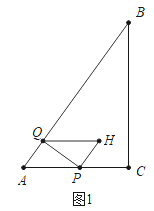
在Rt△ACB中,∵AC=3,AB=5,∠C=90°,
∴BC=![]() =4,
=4,
∵AP=5t,sinA=![]() ,
,
∴![]() ,
,
∴PQ=4t,AQ=![]() =3t.
=3t.
故答案为4t.
(2)如图2中,当点H落在BC上时.
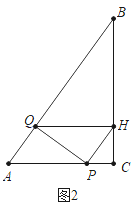
∵QH∥AC,
∴![]() ,
,
∴![]() ,
,
∴t=![]() .
.
(3)①如图3中,当0<t≤![]() 时,重叠部分是四边形APHQ.S=12t2.
时,重叠部分是四边形APHQ.S=12t2.

②如图4中,当![]() ≤t≤
≤t≤![]() 时,重叠部分是四边形ACMQ,
时,重叠部分是四边形ACMQ,
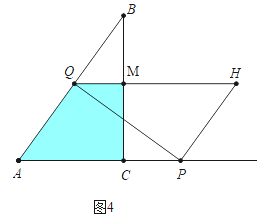
S=![]() =﹣
=﹣![]() t2+
t2+![]() t.
t.
(4)①如图5中,∵S△HEF:S五边形EQAPF=1:7,CD∥PQ,
∴EF是△HPQ的中位线.
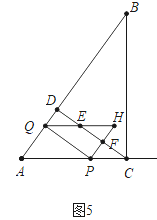
∵cos∠A=![]() ,
,
∴AD=![]() ,
,
∵QH∥AC,
∴∠DQE=∠A,
∴cos∠DQE=cos∠A=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() .
.
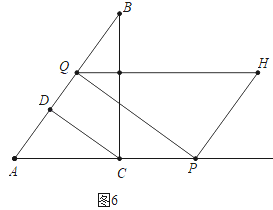
②如图6中,当S△ADC:S五边形CDQHP=1:7时,CD是△APQ的中位线.
∴AQ=2AD,
∴3t=2×![]() ,
,
∴t=![]() .
.
综上所述,满足条件的t的值为![]() 或
或![]() s.
s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(Ⅰ)若设AP=x,则PC= ,QC= ;(用含x的代数式表示)
(Ⅱ)当∠BQD=30°时,求AP的长;
(Ⅲ)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6
 ,CE=4,则DE的长为 .
,CE=4,则DE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,解一元一次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”思想求方程
 =x的解.
=x的解.(3)如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边沿BA、AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

相关试题

