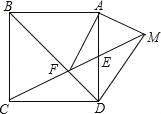
【题目】边长为1的正方形ABCD中,E为边AD的中点,连接线段CE交BD于点F,点M为线段CE延长线上一点,且∠MAF为直角,则DM的长为 .
参考答案:
【答案】![]() .
.
【解析】
试题解析:作MN⊥AD垂足为N.

∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
在△BFA与△BFC中,
 ,
,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME,
∵AE=ED=![]() AD=
AD=![]() ,
,
∴AN=NE=![]() AE=
AE=![]() ,
,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴![]() ,
,
∵CD=1,
∴MN=![]() ,
,
在RT△MND中,∵MN=![]() ,DN=
,DN=![]() ,
,
∴DM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形OABC的边长为12,点A、C分别在x轴、y轴的正半轴上,双曲线y=
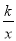 (x>0)与边BC、AD分别交于点D、E,且BD=AE.
(x>0)与边BC、AD分别交于点D、E,且BD=AE.

(1)求k的值;
(2)如图2,若点N为双曲线y=
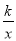 上正方形OABC内部一动点,过点N作y轴的垂线,交AC于点F,交AB于点G,过点F作x轴的垂线交为双曲线y=
上正方形OABC内部一动点,过点N作y轴的垂线,交AC于点F,交AB于点G,过点F作x轴的垂线交为双曲线y= 于点M.设点N的纵坐标为n
于点M.设点N的纵坐标为n①若n=8,求证:△BMN是直角三角形;
②若去掉①中的条件 “n=8”, △BMN是否仍为直角三角形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列等式:x的2倍与10的和等于18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线
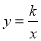 交于点C(1,a).
交于点C(1,a).(1)试确定双曲线的函数表达式;
(2)将l1沿y轴翻折后,得到l2,画出l2的图象,并求出l2的函数表达式;
(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解方程:3x﹣6=﹣31﹣2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳光线下形成的投影是______投影.(平行或中心)
-
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.

(1)求y与x之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
相关试题

