【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
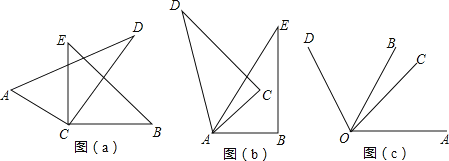
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
参考答案:
【答案】(1)145°,40°,∠ACB+∠DCE=180°,理由见解析;(2)∠DAB+∠CAE=120°,理由见解析;(3)∠AOD+∠BOC=α+β.
【解析】
(1)若∠DCE=35°,根据90°计算∠ACE的度数,再计算∠ACB的度数;若∠ACB=140°,同理,反之计算可得结果;先计算∠ACB=90°+∠BCD,再加上∠DCE可得∠ACB与∠DCE的关系;
(2)先计算∠DAB=60°+∠CAB,再加上∠CAE可得结果;
(3)先计算∠AOD=β+∠COA,再加上∠BOC可得结果.
解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=140°,
∵∠BCE=90°,
∴∠ACE=140°90°=50°,
∵∠ACD=90°,
∴∠DCE=90°50°=40°,
故答案为:145°;40°;
∠ACB+∠DCE=180°,
理由:∵∠ACB=∠ACD+∠BCD=90°+∠BCD,
∴∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°;
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物
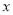 元(
元(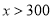 ).
).(1)请用含
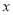 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
-
科目: 来源: 题型:
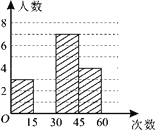
查看答案和解析>>【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a = ,b= ,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
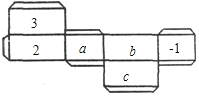
 填空:
填空: 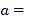 ,
,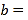 ,
,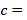 ;
;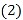 先化简, 再求值:
先化简, 再求值: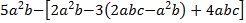 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°, CD⊥AB于点D,∠A=30°,BD=1.5cm ,则AB=______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=
 BC,则△ABC的顶角的度数为_____.
BC,则△ABC的顶角的度数为_____.
相关试题

