【题目】已知△ABC是等腰三角形,∠BAC=90°,CD=![]() BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;
(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证MN⊥AE;
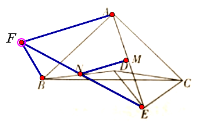
(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索![]() 的值并直接写出结果
的值并直接写出结果
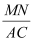
参考答案:
【答案】(1)![]() ;(2)证明过程见解析;(3)
;(2)证明过程见解析;(3)![]() .
.
【解析】
试题分析:(1)根据等腰直角三角形ABC得出BC的长度,然后根据等腰直角三角形DCE得出CE的长度,然后根据Rt△ACE的勾股定理得出AE的长度,从而根据直角三角形斜边上的中线等于斜边的一半得出答案;(2)延长EN到NF,使NE=NF,再连接BF,AF,然后证明△ABF≌△ACE,从而得出∠FAE=∠BAC=90°,然后根据平行线的性质得出答案;(3)根据第二题同样的方法得出MN=![]() AF,AF=AE,从而得出答案.
AF,AF=AE,从而得出答案.
试题解析:(1)∵AB=AC=4 ∠BAC=90° ∴BC=4![]() 则CD=2
则CD=2![]() ∴CE=2,
∴CE=2,
根据Rt△ACE的勾股定理可得:AE=![]() ∴CM=
∴CM=![]()
(2)如图,延长EN到NF,使NE=NF,再连接BF,AF,
可得BF=DE=CE,∠FBN=∠NDE, 则∠ACE=90°-∠DCB
∠ABF=∠BDE-∠ABN=∠180°-∠DBC-∠DCB-∠EDC-∠ABN=180°-(∠DBC+∠ABN)-45°-∠DCB=90°-∠DCB
所以∠ACE=∠ABF,所以△ABF≌△ACE, 所以∠FAB=∠EAC, 所以∠FAE=∠BAC=90°,
因为MN//AF,所以MN⊥AE。
(3)同(2)可得MN=![]() AF,AF=AE,
AF,AF=AE,
又AC=2CE,∠ACE=120°,可求得AE=![]() , 所以
, 所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣1)2n+(﹣1)2n+1的结果为(n为正整数)( )
A.0
B.﹣2
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若ma=mb,则下列等式不一定成立的是( )
A. a=b B. ma+3=mb+3 C. -2ma=-2mb D. ma-2=mb-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x2y)3的结果是( )
A.x5y3
B.x6y
C.3x2y
D.x6y3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中的必然事件是( )
A. 天气阴了之后下雨
B. 小明上学路上看到两车相撞
C. 抛掷一枚骰子,朝上的一面点数恰好是5
D. 同时抛掷两枚骰子,朝上的两面点数之和小于13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果物体向东运动6米记作+6米,那么﹣5米表示的意义是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把5﹣(+2)+(﹣3)﹣(﹣7)写成省略加号和的形式为 .
相关试题

