【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
(1)求抛物线的解析式:
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM周长最短?若不存在,请说明理由;若存在,求出点M的坐标.
参考答案:
【答案】
(1)
解:在y=3x﹣3中,令y=0可求得x=1,令x=0可得y=﹣3,
∴A(1,0),B(0,﹣3),
把A、B两点的坐标分别代入y=x2+bx+c得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=x2+2x﹣3
(2)
解:令y=0得0=x2+2x﹣3,解得x1=1,x2=﹣3
∴C(﹣3,0),AC=4
∴S△ABC= ![]() ACOB=
ACOB= ![]() ×4×3=6
×4×3=6
(3)
解:∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线的对称轴为x=﹣1,
∵A、C关于对称轴对称,
∴MA=MC,
∴MB+MA=MB+MC,
∴当B、M、C三点在同一条直线上时MB+MC最小,此时△ABM的周长最小,
∴连接BC交对称轴于点M,则M即为满足条件的点,

设直线BC的解析式为y=kx+m,
∵直线BC过点B(0,﹣3),C(﹣3,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式y=﹣x﹣3,
当x=﹣1时,y=﹣2,
∴M(﹣1,﹣2),
∴存在点M使△ABM周长最短,其坐标为(﹣1,﹣2)
【解析】(1)由直线解析式可求得A、B两点的坐标,根据待定系数法可求得抛物线解析式;(2)由抛物线解析式可求得C点坐标,再根据三角形的面积可求得答案;(3)连接BC交对称轴于点M,由题意可知A、C关于对称轴对称,则可知MA=MC,故当B、M、C三点在同一条直线上时MA+MB最小,则△ABM的周长最小,由B、C坐标可求得直线BC的解析式,则可求得M点的坐标.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.

(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:BF=2AD;
(2)若CE=
 ,求AC的长.
,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乌苏市某生态示范园,计划种植一批苹果梨,原计划总产量达36万千克,为了满足市场需求,现决定改良苹果梨品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各多少万千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.
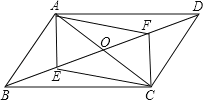
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3﹣2=﹣6
B. =±6
=±6
C.(﹣x)2÷(﹣x)=x
D.(﹣2x2)3=﹣8x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

相关试题

