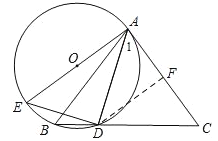
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

参考答案:
【答案】(1)详见解析;(2)⊙O的直径为![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,由AB=AC,AD=DC得∠C=∠B,∠1=∠C,则∠1=∠B,根据圆周角定理得∠E=∠B,∠ADE=90°,所以∠1+∠EAD=90°,然后根据切线的判定定理即可得到AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,根据等腰三角形的性质得CF=![]() AC=3,在Rt△CDF中,利用正弦定义得sinC=
AC=3,在Rt△CDF中,利用正弦定义得sinC=![]() =
=![]() ,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
试题解析:(1)∵AB=AC,AD=DC,
∴∠C=∠B,∠1=∠C,
∴∠1=∠B,
又∵∠E=∠B,
∴∠1=∠E,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠1+∠EAD=90°,即∠EAC=90°,
∴AE⊥AC,
∴AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,
∵DA=DC,
∴CF=![]() AC=3,
AC=3,
在Rt△CDF中,∵sinC=![]() =
=![]() ,
,
设DF=4x,DC=5x,
∴CF=![]() =3x,
=3x,
∴3x=3,解得x=1,
∴DC=5,
∴AD=5,
∵∠ADE=∠DFC=90°,∠E=∠C,
∴△ADE∽△DFC,
∴![]() ,即
,即![]() ,解得AE=
,解得AE=![]() ,
,
即⊙O的直径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
已知a2﹣a﹣5=0,求(3a2﹣7a)﹣2(a2﹣3a+2)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是( )
A.正方形
B.长方形
C.线段
D.梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算-3+2的结果是( )
A.1
B.-1
C.5
D.-5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,是一列用若干根火柴棒摆成的由正方形组成的图案.
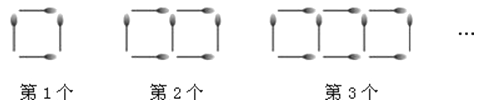
(1)完成下表的填空:正方形个数
1
2
3
4
5
6
n
火柴棒根数
4
7
10
13
(2)某同学用若干根火柴棒按如上图列的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,…,当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第n+1个图案还差2根.问最后摆的图案是第几个图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果零上15℃记作+15℃,那么零下5℃应记作( ).
A.-5℃B.-20℃C.+5℃D.+20℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若四边形AEDF的周长为24,AB=15,求AC的长;
(2)求证:EF垂直平分AD.

相关试题

