【题目】如图,冬生、夏亮两位同学从学校出发到青年路小学参加现场作为比赛,冬生步行一段时间后,夏亮骑自行车沿相同路线行进,两人都是匀速前进,他们的路程差s(米)与冬生出发时间t(分)之间的函数关系如图所示.
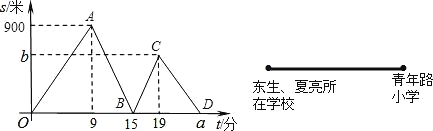
根据图象进行以下探究:
(1)冬生的速度是 米/分,请你解释点B坐标(15,0)所表示的意义: ;
(2)求夏亮的速度和他们所在学校与青年路小学的距离;
(3)求a,b值及线段CD所表示的y与x之间的函数关系,并写出自变量的取值范围.
参考答案:
【答案】(1)100,冬生出发15分时,夏亮追上冬生;(2)2500米;
(3)y=﹣100x+2500(19≤x≤25).
【解析】
试题分析:(1)由图象可知,0~8分时为冬生步行,根据速度=路程÷时间求出冬生的速度;点B所表示的意义:冬生出发15分时,夏亮追上冬生;
(2)根据15分时,夏亮追上冬生,利用追击问题的等量关系求出夏亮的速度,再根据路程=速度×时间列式计算即可夏亮运动的距离,即他们所在学校与青年路小学的距离;
(3)根据路程=速度×时间列式计算即可求出a、b,最后根据待定系数法即可求得线段CD所表示的y与x之间的函数关系.
试题解析:(1)冬生的速度:900÷9=100米/分,
点B所表示的意义:冬生出发15分时,夏亮追上冬生;
故答案为:100,冬生出发15分时,夏亮追上冬生;
(2)当冬生出发15分时,夏亮运动了15﹣9=6(分),运动的距离是:15×100=1500(米),
∴夏亮的速度:1500÷6=250(米/分),
当第19分以后两人距离越来越近,说明夏亮已到达终点,故夏亮先到达青年路小学,此时夏亮运动的时间为19﹣9=10(分),运动的距离为10×250=2500(米),
故他们所在学校与青年路小学的距离是2500米;
(3)由(1)(2)可知,两所学校相距2500米,冬生的速度是100米/分,
故a=![]() =25,b=100×(25﹣19)=600,
=25,b=100×(25﹣19)=600,
设线段CD所表示的y与x之间的函数关系为y=kx+b,由题意得
![]() ,解得
,解得![]() .
.
故y=﹣100x+2500(19≤x≤25).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
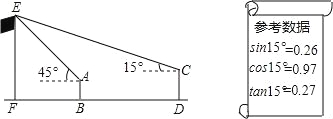
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距600 km,甲车以60 km/h的速度从A地驶向B地,2 h后,乙车以100 km/h的速度沿着相同的道路从A地驶向B地.设乙车出发x小时后追上甲车,根据题意可列方程为( )
A. 60(x+2)=100x
B. 60x=100(x-2)
C. 60x+100(x-2)=600
D. 60(x+2)+100x=600
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3x2y2(﹣2xy3)
(2)(x﹣y)(x2+xy﹣y2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x+6>3x+4的正整数解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角为 40°,则它的底角的度数为( )
A. 40° B. 70° C. 40°或 70° D. 80°
-
科目: 来源: 题型:
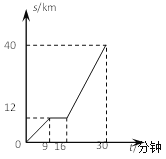
查看答案和解析>>【题目】如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。观察图中所提供的信息,解答下列问题:
(1)求汽车在前9分钟内的平均速度.
(2)汽车在中途停留的时间.
(3)求该汽车行驶30千米的时间.
相关试题

