【题目】有理数a,b在数轴上的对应点位置如图所示:
![]()
(1)化简:∣a∣+∣a+b∣-2∣a-b∣
(2)若a与-![]() 的距离等于b与-
的距离等于b与-![]() 的距离,求-3(a+b)+5的值.
的距离,求-3(a+b)+5的值.
参考答案:
【答案】(1)-3b;(2)7.
【解析】
(1)根据数轴,确定a、a+b,a-b的正负,然后去绝对值化简即可;(2)由数轴可得a<-![]() ,b>-
,b>-![]() ,设a与-
,设a与-![]() 的距离为x,则a=-
的距离为x,则a=-![]() -x,b=-
-x,b=-![]() +x,然后代入-3(a+b)+5求值即可.
+x,然后代入-3(a+b)+5求值即可.
解:(1)由数轴可得a<0,b>0,a+b<0,a-b<0
则∣a∣+∣a+b∣-2∣a-b∣
=-a-(a+b)+2(a-b)
=-a-a-b+2a-2b
=-3b
(2) 由数轴可得a<-![]() ,b>-
,b>-![]() ,设a与-
,设a与-![]() 的距离为x,则a=-
的距离为x,则a=-![]() -x,b=-
-x,b=-![]() +x;
+x;
将其代入-3(a+b)+5=-3×(-![]() -x+-
-x+-![]() +x)+5=-3×(-
+x)+5=-3×(-![]() )+5=2+5=7.
)+5=2+5=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲
25
30
乙
45
60
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数
 (k≠0)的图象上.
(k≠0)的图象上.(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】自实施新教育改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分同学进行了为期半个月的跟踪调查,并将调查结果分为四类:A.特别好;B.好;C.一般;D.较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了多少名同学?
(2)求出调查中C类女生及D类男生的人数,将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.

(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为
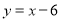 ,求三角线ACE的面积.
,求三角线ACE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点P作PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用
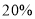 的材料.
的材料.(1)求制作每个甲种边框、乙种边框各用多少米材料?
(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?
相关试题

