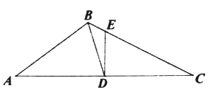
【题目】如图,![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积为54,则线段
的面积为54,则线段![]() 的长为__________.
的长为__________.
参考答案:
【答案】6![]()
【解析】
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M,根据DE垂直平分AC,从而证出![]() ,再根据
,再根据![]() ,从而证出
,从而证出![]() ,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据
,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据![]() ,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt
,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt![]() 中,根据勾股定理得出x和y的关系,再根据
中,根据勾股定理得出x和y的关系,再根据![]() 的面积为54,所以有
的面积为54,所以有![]() 的面积也为54,所以
的面积也为54,所以![]() ,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M.

∵DE垂直平分AC
∴BM//DE
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵BM⊥AC,CN⊥AB
∴MC=CN
设AB=x,DM=y
∵AB=AD, DE垂直平分AC
∴AD=CD=x,CN=x+y
∵![]() 的面积为54
的面积为54
∴![]() 的面积也为54
的面积也为54
∴![]()
∵![]() ,
,![]()
∴![]()
∴AB:AC=AM:AN=1: 2
∴AN=2AM=2(x-y)
在Rt![]() 中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
解得,x=5y或x=y(不合题意舍去)
∵![]()
∴xy=36
在Rt![]() 中,BM2=x2—(x-y)2
中,BM2=x2—(x-y)2
在Rt![]() 中,BD2=x2-(x-y)2+y2=2xy
中,BD2=x2-(x-y)2+y2=2xy
∴BD2=72,
∴BD=6![]()
故答案为:6![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
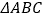 中,
中,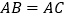 ,
,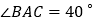 ,点
,点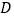 在直线
在直线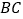 上,
上,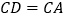 ,则
,则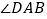 的度数为_______.
的度数为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条长度均为2的线段
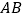 和线段
和线段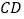 互相重合,将
互相重合,将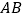 沿直线
沿直线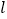 向左平移
向左平移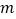 个单位长度,将
个单位长度,将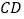 沿直线
沿直线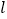 向右也平移
向右也平移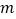 个单位长度,当
个单位长度,当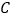 、
、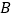 是线段
是线段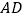 的三等分点时,则
的三等分点时,则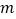 的值为________.
的值为________.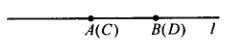
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)【参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70】

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一张边长为
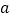 厘米的正方形桌面,因为实际需要,需将正方形边长增加
厘米的正方形桌面,因为实际需要,需将正方形边长增加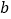 厘米,木工师傅设计了如图所示的三种方案:
厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:
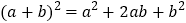 .
.对于方案一,小明是这样验证的:
 大正方形面积可表示为:
大正方形面积可表示为: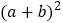 ,也可以表示为:
,也可以表示为: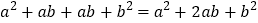 ,
, .
.请你仿照上述方法根据方案二、方案三,写出公式的验证过程.
(1)方案二:
(2)方案三:
-
科目: 来源: 题型:
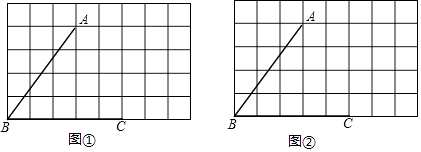
查看答案和解析>>【题目】图①、图②是8×5的正方形网格,线段AB、BC的端点均在格点上.按要求在图①、图②中以AB、BC为邻边各画一个四边形ABCD,使点D在格点上.要求所画两个四边形不全等,且同时满足四边形ABCD是轴对称图形,点D到∠ABC两边的距离相等.
相关试题

