Question

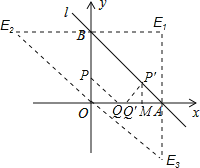
【题目】如图，直线l与坐标轴分别交于A、B两点，∠BAO=45°，点A坐标为（8，0）．动点P从点O出发，沿折线段OBA运动，到点A停止；同时动点Q也从点O出发，沿线段OA运动，到点A停止；它们的运动速度均为每秒1个单位长度．

（1）求直线AB的函数关系式；

（2）若点A、B、O与平面内点E组成的图形是平行四边形，请直接写出点E的坐标；

（3）在运动过程中，当P、Q的距离为2时，求点P的坐标．

Answer 1

【答案】（1）y=﹣x+8；（2）见解析；（3）P′（8﹣，）．

【解析】

试题分析：（1）设直线AB解析式为y=kx+b，将A与B坐标代入求出k与b的值，即可确定出解析式；

（2）考虑三种情况，如图所示，四边形AOBE1为平行四边形时；四边形ABE2O为平行四边形时；四边形ABOE3为平行四边形时，分别求出E的坐标即可；

（3）分两种情况考虑：当P在OB上时，连接PQ，根据PQ的长及三角形OPQ为等腰直角三角形，求出OP的长，确定出此时P坐标；当P′在AB上时，过P′作P′M⊥x轴，确定出此时P′坐标即可．

解：（1）∵∠BAO=45°，∠AOB=90°，

∴△AOB为等腰直角三角形，即OA=OB=8，

∴B（0，8），

设直线AB解析式为y=kx+b，

将A（8，0）与B（0，8）代入得：，

解得：k=﹣1，b=8，

则直线AB解析式为y=﹣x+8；

（2）如图所示：当四边形AOBE1为平行四边形时，E1坐标为（8，8）；

当四边形ABE2O为平行四边形时，E2坐标为（﹣8，8）；

当四边形ABOE3为平行四边形时，E3坐标为（8，﹣8）；

（3）当P在OB上时，连接PQ，由PQ=2，

在Rt△POQ中，OP=OQ，可得：OP=OQ=×2=，此时P（0，）；

当P′在AB上时，过P′作P′M⊥x轴，

∵P′Q′=2，△P′Q′M为等腰直角三角形，

∴P′M=Q′M=，OM=OB﹣P′M=8﹣，

此时P′（8﹣，）．