【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到∠BOD=180°-54°=126°,然后由弧长的公式即可计算出结果.
试题解析:(1)连接OD,BD,
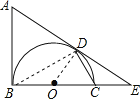
∵AB是⊙O的切线,∴AB⊥BC,即∠ABO=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°;
又∵OD是圆O的半径,∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠COD
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO=2∠CDE,
∴∠A=2∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°,
∵OB=2,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB,BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A.点O在AC的垂直平分线上
B.△AOB,△BOC,△COA都是等腰三角形
C.∠OAB+∠OBC+∠OCA=90°
D.点O到AB,BC,CA的距离相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法,错误的是( )
A.为了解一种灯泡的使用寿命,宜采用普查的方法
B.一组数据8,8,7,10,6,8,9的众数是8
C.方差反映了一组数据与其平均数的偏离程度
D.对于简单随机样本,可以用样本的方差去估计总体的方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商店将A品牌彩电按成本价提高50%,然后在广告上写“大酬宾,八折优惠”,结果每台A品牌彩电仍获利300元,则每台A品牌彩电的成本价是_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2 , y=﹣2x2 , y=2x2+1共有的性质是( )
A.开口向上
B.对称轴都是y轴
C.都有最高点
D.顶点都是原点 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )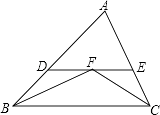
A.①②③
B.①②③④
C.①②
D.① -
科目: 来源: 题型:
查看答案和解析>>【题目】对乘积(﹣3)×(﹣3)×(﹣3)×(﹣3)记法正确的是( )
A. ﹣34B. (﹣3)4C. ﹣(+3)4D. ﹣(﹣3)
相关试题

